Trigonometrical Ratios of 45°

How to find the trigonometrical Ratios of 45°?

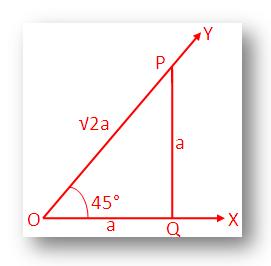
Let a rotating line \(\overrightarrow{OX}\) rotates about O in the anti-clockwise sense and starting from the initial position \(\overrightarrow{OX}\) traces out ∠AOB = 45°.

Take a point P on \(\overrightarrow{OY}\) and draw \(\overline{PQ}
\) perpendicular to \(\overrightarrow{OX}\).

Now, ∠OPQ = 180° - ∠POQ - ∠PQO

= 180° - 45° - 90°

= 45°.

Therefore, in the △OPQ we have, ∠QOP = ∠OPQ.

Therefore, PQ = OQ = a (say).

Now,

OP² = OQ² + PQ²

OP² = a² + a²

OP² = 2a²

Therefore,  \(\overline{OP}\) = √2 a (Since, \(\overline{OP}\) is positive)

Therefore, from the right-angled △OPQ we get,

sin  45° = \(\frac{\overline{PQ}}{\overline{OP}} = \frac{a}{\sqrt{2} a} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}\)

cos  45° = \(\frac{\overline{OQ}}{\overline{OP}} = \frac{a}{\sqrt{2} a} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}\)

And tan  45° = \(\frac{\overline{PQ}}{\overline{OQ}} = \frac{a}{a} = 1\).

Clearly, csc  45° = \(\frac{1}{sin  45°}\) = √2,

sec  45° = \(\frac{1}{cos  45°}\) = √2

And  cot  45° = \(\frac{1}{tan  45°}\) = 1

Trigonometrical Ratios of 45° are commonly called standard angles and the trigonometrical ratios of these angles are frequently used to solve particular angles.

● Trigonometric Functions

• Basic Trigonometric Ratios and Their Names
• Restrictions of Trigonometrical Ratios
• Reciprocal Relations of Trigonometric Ratios
• Quotient Relations of Trigonometric Ratios
  
• Limit of Trigonometric Ratios
  
• Trigonometrical Identity
• Problems on Trigonometric Identities
• Elimination of Trigonometric Ratios
• Eliminate Theta between the equations
• Problems on Eliminate Theta
• Trig Ratio Problems
• Proving Trigonometric Ratios
• Trig Ratios Proving Problems
• Verify Trigonometric Identities
• Trigonometrical Ratios of 0°
• Trigonometrical Ratios of 30°
• Trigonometrical Ratios of 45°
• Trigonometrical Ratios of 60°
• Trigonometrical Ratios of 90°
• Trigonometrical Ratios Table
• Problems on Trigonometric Ratio of Standard Angle
  
• Trigonometrical Ratios of Complementary Angles
• Rules of Trigonometric Signs
• Signs of Trigonometrical Ratios
  
• All Sin Tan Cos Rule
• Trigonometrical Ratios of (- θ)
• Trigonometrical Ratios of (90° + θ)
• Trigonometrical Ratios of (90° - θ)
• Trigonometrical Ratios of (180° + θ)
• Trigonometrical Ratios of (180° - θ)
• Trigonometrical Ratios of (270° + θ)
• Trigonometrical Ratios of (270° - θ)
• Trigonometrical Ratios of (360° + θ)
• Trigonometrical Ratios of (360° - θ)
• Trigonometrical Ratios of any Angle
• Trigonometrical Ratios of some Particular Angles
• Trigonometric Ratios of an Angle
• Trigonometric Functions of any Angles
• Problems on Trigonometric Ratios of an Angle
• Problems on Signs of Trigonometrical Ratios

11 and 12 Grade Math

From Trigonometrical Ratios of 45° to HOME PAGE