Triangle on Same Base and between Same Parallels
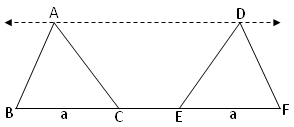
Triangle on same base and between same parallels is equal in area.
In the adjoining figure, ∆ABD and ∆DEF are having equal base ‘a cm’ and are between the same parallels BF and AD.
Therefore, area of ∆ABD = Area of ∆DEF
Prove that the triangles on same base and between same parallels are equal in area.
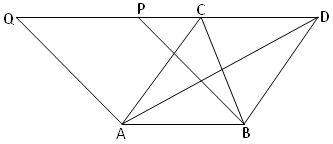
Let ∆ABC and ∆ABD be on the same
base AB and between the same parallel AB and CD. It is require to prove that ∆ABC
= ∆ABD.
Construction: A parallelogram ABPQ is constructed with AB as base and lying between the same parallels AB and CD.
Proof: Since ∆ABC and parallelogram ABPQ are on the same base AB and between the same parallels AB and Q,
Therefore, ∆ABC = ½(Parallelogram ABPQ)
Similarly, ∆ABD = ½(Parallelogram ABPQ)
Therefore, ∆ABC = ∆ABD.
Note: Since the relationship between the areas of a triangle and a parallelogram on the same base and between the same parallels in known to us, so that parallelogram ABPQ is constructed]
Solved examples for the triangle on same base and between same parallels:
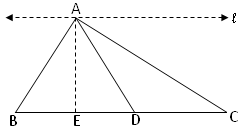
1. Shaw that the medians of the triangle divide it into triangles of equal area.
Solution:
AD is the median of the ∆ABC and AE is the altitude of ∆ABC and also ∆ADC.
(AE ┴ BC)
AD is the median of ABC
Therefore, BD = DC
Multiply both sides by AE,
Then BD × AE = DC × AE
1/2 BD × AE = 1/2 DC × AE
Area of ∆ABD = Area of ∆ADC
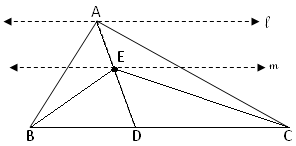
2. AD is the median of ∆ABC and ∆ADC. E is any point on AD. Show that area of ∆ABE = area of ∆ACE.
Solution:
Since, AD is the median of ∆ABC, therefore BD = DC
Since, ∆ABD and ∆ADC have equal bases BD = DC and are between the same parallels BC and l,
Therefore Area of ∆ABD = Area of ∆ADC
Since, E lies on AD,
Therefore, ED is the median of the BEC
Now, BED and CED have equal bases BD = DC and between the same parallels BC and m.
Therefore, area of ∆BED = Area of ∆CED
On subtracting (1) and (2), we get
Area of ∆ABD - Area of ∆BED = Area of ∆ACD - Area of ∆CED
Area of ∆ABE = Area of ∆ACE
Figure on Same Base and between Same Parallels
Parallelograms on Same Base and between Same Parallels
Parallelograms and Rectangles on Same Base and between Same Parallels
Triangle and Parallelogram on Same Base and between Same Parallels
Triangle on Same Base and between Same Parallels
8th Grade Math Practice
From Triangle on Same Base and between Same Parallels to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Multiplication Table | Learn Tables from 0 – 25 | Multiplication Table
Jan 14, 25 11:53 PM
In math multiplication table we will learn the tables from 0 – 25. These multiplication tables help the students to learn the essential multiplication facts. Multiplication tables are very important f… -
3rd Grade Math Worksheets |3rd Grade Math Sheets|3rd Grade Math Lesson
Jan 14, 25 11:02 PM
3rd grade math worksheets is carefully planned and thoughtfully presented on mathematics for the students. Teachers and parents can also follow the worksheets to guide the students. -
3rd Grade Subtraction Worksheet | 3-Digit Subtraction Worksheets | Ans
Jan 14, 25 01:57 PM
In 3th Grade Addition Worksheet we will solve how to subtract 3-digit numbers by expansion, subtraction of 3-digit numbers without regrouping, subtraction of 3-digit numbers with regrouping, propertie… -
Facts about Subtraction | Subtraction of Small Numbers|Solved Examples
Jan 14, 25 12:29 AM
The operation to finding the difference between two numbers is called subtraction. Let us know some facts about subtraction which will help us to learn subtraction of large numbers. 1. Subtraction wit… -
Word Problems on Subtraction |Worksheet on Subtraction Word Problems |
Jan 14, 25 12:21 AM
In word problems on subtraction we need to read the question carefully and understand what we need to find out. We know, in subtraction the larger number from which we subtract the other number (the s…
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.