Square Root of Number in the Fraction Form

In square root of number in the fraction form, suppose the square root of a fraction $\frac{x}{a}$ is that fraction $\frac{y}{a}$ which when multiplied by itself gives the fraction $\frac{x}{a}$.

If x and y are squares of some numbers then,

$\sqrt{\frac{x}{y}} = \frac{\sqrt{x}}{\sqrt{y}}$

If the fraction is expressed in a mixed form, convert it into improper fraction. 

Find the square root of numerator and denominator separately and write the answer in the fraction form.

Examples on square root of number in the fraction form are explained below;

1. Find the square root of $\frac{625}{256}$

Solution:

$\sqrt{\frac{625}{256}} = \frac{\sqrt{625}}{\sqrt{256}}$

Now, we find the square roots of 625 and 256 separately.

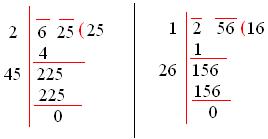
Thus, √625 = 25 and √256 = 16

⇒ $\sqrt{\frac{625}{256}} = \frac{\sqrt{625}}{\sqrt{256}}$ = $\frac{25}{26}$

2. Evaluate: $\sqrt{\frac{441}{961}}$.

Solution:

$\sqrt{\frac{441}{961}} = \frac{\sqrt{441}}{\sqrt{961}}$

Now, we find the square roots of 441 and 961 separately.

Thus, √441 = 21 and √961 = 31

⇒ $\sqrt{\frac{441}{961}}$ = $\frac{\sqrt{441}}{\sqrt{961}}$ = $\frac{21}{31}$

3. Find the values of $\sqrt{\frac{7}{2}}$ up to 3 decimal places. 

Solution:

To make the denominator a perfect square, multiply the numerator and denominator by √2.

Therefore, $\frac{\sqrt{7} \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}}$ = $\frac{\sqrt{14}}{2}$

Now, we find the square roots of 14 up to 3 places of decimal.

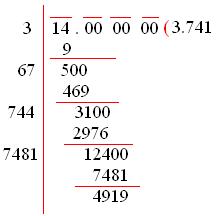
Thus, √14 = 3.741 up to 3 places of decimal.

                  = 3.74 correct up to 2 places of decimal.

Therefore, $\frac{\sqrt{14}}{2}$ = $\frac{3.74}{2}$ = 1.87. 

4. Find the square root of 1$\frac{56}{169}$

Solution: 

1$\frac{56}{169}$ = $\frac{225}{169}$

Therefore, $\sqrt{1\frac{56}{169}}$ = $\sqrt{\frac{225}{169}} = \frac{\sqrt{225}}{\sqrt{169}}$

We find the square roots of 225 and 169 separately

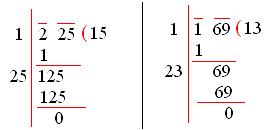
Therefore, √225 = 15 and √169 = 13

⇒ $\sqrt{1\frac{56}{169}}$ = $\sqrt{\frac{225}{169}} = \frac{\sqrt{225}}{\sqrt{169}}$ = $\frac{15}{13}$ = 1$\frac{2}{13}$

5. Find the value of $\frac{\sqrt{243}}{\sqrt{363}}$.

Solution: 

$\frac{\sqrt{243}}{\sqrt{363}}$ = $\sqrt{\frac{243}{363}}$  = $\sqrt{\frac{81}{121}} = \frac{\sqrt{81}}{\sqrt{121}}$ = $\frac{9}{11}$ 

6. Find out the value of √45 × √20.

Solution:

√45 × √20 = √(45 × 20)

                   = √(3 × 3 × 5 × 2 × 2 × 5)

                   = √(3 × 3 × 2 × 2 × 5 × 5 )

                   = (3 × 2 × 5)

                   = 30.

● Square Root

Square Root

Square Root of a Perfect Square by using the Prime Factorization Method

Square Root of a Perfect Square by Using the Long Division Method

Square Root of Numbers in the Decimal Form

Square Root of Number in the Fraction Form

Square Root of Numbers that are Not Perfect Squares

Table of Square Roots

Practice Test on Square and Square Roots

● Square Root- Worksheets

Worksheet on Square Root using Prime Factorization Method

Worksheet on Square Root using Long Division Method

Worksheet on Square Root of Numbers in Decimal and Fraction Form

8th Grade Math Practice

From Square Root of Number in the Fraction Form to HOME PAGE