Square Root of a Perfect Square by using the Prime Factorization Method

To find the square root of a perfect square by using the prime factorization method when a given number is a perfect square:

Step I: Resolve the given number into prime factors.

Step II: Make pairs of similar factors.

Step III: Take the product of prime factors, choosing one factor out of every pair.

Examples on square root of a perfect square by using the prime factorization method:

1. Find the square root of 484 by prime factorization method.

Solution:

Resolving 484 as the product of primes, we get

484 = 2 × 2 × 11 × 11 

√484 = √(2 × 2 × 11 × 11) 

= 2 × 11

Therefore, √484 = 22

2. Find the square root of 324.

Solution:

The square root of 324 by prime factorization, we get

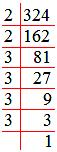
324 = 2 × 2 × 3 × 3 × 3 × 3

√324 = √(2 × 2 × 3 × 3 × 3 × 3)

= 2 × 3 × 3


Therefore, √324 = 18



3. Find out the square root of 1764.

Solution:

The square root of 1764 by prime factorization, we get

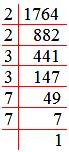
1764 = 2 x 2 x 3 x 3 x 7 x 7.

√1764 = √(2 x 2 x 3 x 3 x 7 x 7)

= 2 x 3 x 7




Therefore, √1764 = 42.



4. Evaluate √4356

Solution:

By using prime factorization, we get

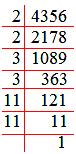
4356 = 2 x 2 x 3 x 3 x 11 x 11

√4356 = √(2 x 2 x 3 x 3 x 11 x 11)

= 2 × 3 × 11




Therefore, √4356 = 66.



5. Evaluate √11025

Solution:

By using prime factorization, we get

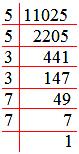
11025 = 5 x 5 x 3 x 3 x 7 x 7.

√11025 = √(5 x 5 x 3 x 3 x 7 x 7)

= 5 × 3 × 7





Therefore, √11025 = 105

6. In an auditorium, the number of rows is equal to the number of chairs in each row. If the capacity of the auditorium is 2025, find the number of chairs in each row.

Solution:

Let the number of chairs in each row be x.

Then, the number of rows = x.

Total number of chairs in the auditorium = (x × x) = x²

But, the capacity of the auditorium = 2025 (given).

Therefore, x² = 2025

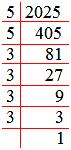
= 5 × 5 × 3 × 3 × 3 × 3

x = (5 × 3 × 3) = 45.






Hence, the number of chairs in each row = 45

7. Find the smallest number by which 396 must be multiplied so that the product becomes a perfect square.

Solution:

By prime factorization, we get

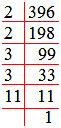
396 = 2 × 2 × 3 × 3 × 11

It is clear that in order to get a perfect square, one more 11 is required.

So, the given number should be multiplied by 11 to make the product a perfect square.




8. Find the smallest number by which 1100 must be divided so that the quotient is a perfect square.

Solution:

Expressing 1100 as the product of primes, we get

1100 = 2 × 2 × 5 × 5 × 11

Here, 2 and 5 occur in pairs and 11 does not.

Therefore, 1100 must be divided by 11 so that the quotient is 100

i.e., 1100 ÷ 11 = 100 and 100 is a perfect square.



9. Find the least square number divisible by each one of 8, 9and 10.

Solution:

The least number divisible by each one of 8, 9, 10 is their LCM.

Now, LCM of 8, 9, 10 = (2 × 4 × 9 × 5) = 360

By prime factorization, we get

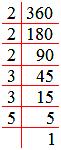
360 = 2 × 2 × 2 × 3 × 3 × 5

To make it a perfect square it must be multiplied by (2 × 5) i.e., 10.





Hence, the required number = (360 × 10) = 3600.

● Square Root

Square Root

Square Root of a Perfect Square by using the Prime Factorization Method

Square Root of a Perfect Square by Using the Long Division Method

Square Root of Numbers in the Decimal Form

Square Root of Number in the Fraction Form

Square Root of Numbers that are Not Perfect Squares

Table of Square Roots

Practice Test on Square and Square Roots

● Square Root- Worksheets

Worksheet on Square Root using Prime Factorization Method

Worksheet on Square Root using Long Division Method

Worksheet on Square Root of Numbers in Decimal and Fraction Form

8th Grade Math Practice

From Square Root of a Perfect Square by using the Prime Factorization Method to HOME PAGE