Slope of the Line Joining Two Points
We will discuss here about the slope of the line joining two points.
To find the slope of a non-vertical straight line passing through two given fixed points:
Let P (x1, y1) and Q (x2, y2) be the two given points. According to the problem, the straight line PQ is non-vertical x2 ≠ x1.
Required to find, the slope of the line through P and Q.
From P, Q draw perpendiculars PM, QN on x-axis and PL ⊥ NQ. Let θ be the inclination of the line PQ, then ∠LPQ = θ.
From the above diagram, we have
PL = MN = ON - OM = x2 - x1 and
LQ = = NQ - NL = NQ - MP = y2 - y1
Therefore, the slope of the line PQ = tan θ
= LQPL
= y2−y1x2−x1
= DifferenceofordinatesofthegivenpointsDifferenceoftheirabscissae
Hence, the slope (m) of a non-vertical line passing through the points P (x1, y1) and Q (x2, y2) is given by
slope = m = y2−y1x2−x1
1. Find the slope of the line passing through the points M (-2, 3) and N (2, 7).
Solution:
Let M (-2, 3) = (x1, y1) and N (2, 7) = (x2, y2)
We know that the slope of a straight line passing through two points (x1, y1) and (x2, y2) is
m = y2−y1x2−x1
Therefore, slope of MN = y2−y1x2−x1 = 7−32+2 = 44 = 1.
2. Find the slope of the line passing through the pairs of points (-4, 0) and origin.
Solution:
We know that the coordinate of the origin is (0, 0)
Let P (-4, 0) = (x1, y1) and O (0, 0) = (x2, y2)
We know that the slope of a straight line passing through two points (x1, y1) and (x2, y2) is
m = y2−y1x2−x1
Therefore, slope of PO = y2−y1x2−x1
= 0−(00−(−4)
= 04
= 0.
● Equation of a Straight Line
- Inclination of a Line
- Slope of a Line
- Intercepts Made by a Straight Line on Axes
- Slope of the Line Joining Two Points
- Equation of a Straight Line
- Point-slope Form of a Line
- Two-point Form of a Line
- Equally Inclined Lines
- Slope and Y-intercept of a Line
- Condition of Perpendicularity of Two Straight Lines
- Condition of parallelism
- Problems on Condition of Perpendicularity
- Worksheet on Slope and Intercepts
- Worksheet on Slope Intercept Form
- Worksheet on Two-point Form
- Worksheet on Point-slope Form
- Worksheet on Collinearity of 3 Points
- Worksheet on Equation of a Straight Line
From Intercepts Made by a Straight Line on Axes to HOME
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Counting Numbers from 1 to 50 | Match the Number | Missing Numbers
Apr 04, 25 03:46 PM
In counting numbers from 1 to 50, recognize the numbers, count and then join the numbers in the correct number order. Here we mainly need eye-hand coordination to draw the picture and maintain the num -
Counting Eleven to Twenty with Numbers and Words |Numbers from 11 - 20
Apr 04, 25 03:21 PM
Counting eleven to twenty with numbers and words are explained below. One ten and one more is eleven. Eleven comes after ten. One ten and two more is twelve. Twelve comes after eleven. -
5th Grade BODMAS Rule Worksheet | PEMDAS | Order of operations|Answers
Apr 03, 25 03:11 PM
In 5th Grade BODMAS Rule Worksheet you will get different types of problems on mathematical expressions involving different operations, mathematical expression with 'brackets' and 'of' and simplifying… -
Worksheet on Simplification | Simplify Expressions | BODMAS Questions
Apr 03, 25 02:58 PM
In worksheet on simplification, the questions are based in order to simplify expressions involving more than one bracket by using the steps of removal of brackets. This exercise sheet -
Divisible by 2 Video |Test of Divisibility by 2 Trick| Rules| Examples
Apr 03, 25 10:25 AM
A number is divisible by 2 if the digit at unit place is either 0 or multiple of 2. So a number is divisible by 2 if digit at its units place is 0, 2, 4, 6 or 8.
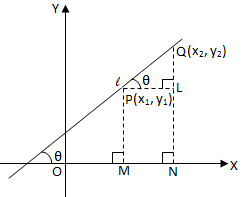




New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.