Simplification of Fractions
In simplification of fractions parenthesis can also be used. The three parenthesis (1st), {2nd}, [3rd] are used commonly.
Examples on simplification of fractions:
1. 3 1/3 ÷ 5/3 - 1/10 of 2 ½ + 7/4
Solution:
3 1/3 ÷ 5/3 - 1/10 of 2 ½ + 7/4
= (3 × 3 + 1)/3 ÷ 5/3 – 1/10 of (2 × 2 + 1)/2 + 7/4
= 10/3 ÷ 5/3 - 1/10 of 5/2 + 7/4
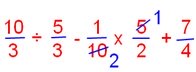
[‘of’ simplified]
= 10/3 × 3/5 – ½ × ½ + 7/4 [‘÷’ simplified]
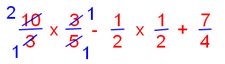
= 2/1 - ¼ + 7/4 [‘×’ simplified]
= (2 × 4)/(1 × 4) - (1 × 1)/(4 × 1) + (7 × 1)/(4 × 1)
= 8/4 - ¼ + 7/4
[Now the denominators are same of all the fractions]
= (8 – 1 + 7)/4 [‘+’ and ‘-‘ simplified]
= 14/4
= 7/2
= 3\(\frac{1}{2}\)
2. 45 of 3/5 ÷ 1 2/3 + 3 of 1/3 – 10
Solution:
45 of 3/5 ÷ 1 2/3 + 3 of 1/3 – 10
= 45 of 3/5 ÷ (1 × 3 + 2)/3 + 3 of 1/3 – 10
= 45 of 3/5 ÷ 5/3 + 3 of 1/3 – 10
= 45 × 3/5 ÷ 5/3 + 3 × 1/3 – 10 [‘of’ simplified]
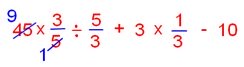
= 9 × 3 × 3/5 + 3 × 1/3 – 10 [‘÷’ simplified], [‘×’ simplified]
= (27 × 3)/5 + 1 – 10
= 81/5 + 1 – 10
= (81 × 1)/(5 × 1) + (1 × 5)/(1 × 5) – (10 × 5)/(1 × 5)
= 81/5 + 5/5 – 50/5
[Now the denominators are same of all the fractions]
= (81 + 5 – 50)/5 [‘+’ and ‘-‘ simplified]
= 36/5
= 7 1/5
43 of 1/86 ÷ 1/14 × 2/7 + 9/4 – ¼
Solution:
43 of 1/86 ÷ 1/14 × 2/7 + 9/4 – ¼
= 43 × 1/86 ÷ 1/14 × 2/7 + 9/4 – ¼
= 2/1 + 9/4 – ¼
= (2 × 4)/(1 × 4) + (9 × 1)/(4 × 1) - (1 × 1)/(4 × 1)
= 8/4 + 9/4 - 1/4
[Now the denominators are same of all the fractions]
= (8 + 9 - 1)/4
= 16/4
= 4
4. 9/10 ÷ (3/5 + 2 1/10)
Solution:
9/10 ÷ (3/5 + 2 1/10)
= 9/10 ÷ (3/5 + 21/10)
= 9/10 ÷ ((6 +21)/10)
[Solve within brackets]
= 9/10 ÷ 27/10
= 9/10 × 10/27
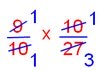
= 1/3
5. (7 ¼ - 6 1/4) of (2/5 + 3/15)
Solution:
(7 ¼ - 6 1/4) of (2/5 + 3/15)
= (29/4 – 25/4) of (2/5 + 3/15)
= ((29 – 25)/4) × ((6 + 3)/15)
[Solve within brackets]
= 4/4 × 9/15
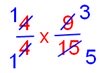
[Reduce to lowest term]
= 1 × 3/5
= 3/5
6. {18 + (2 ½ + 4/5)} of 1/1000
Solution:
{18 + (2 ½ + 4/5)} of 1/1000
= {18 + (5/2 + 4/5)} of 1/1000
= {18 + ((25 + 8)/10)} of 1/1000
= {18 + 33/10} of 1/1000
= {(180 + 33)/10} of 1/1000
= 213/10 of 1/1000
= 213/10 × 1/1000
= (213 × 1)/(10 × 1000)
= 213/10000
= 0.0213
These are the examples of simplification of fractions.
● Multiplication is Repeated Addition.
● Multiplication of Fractional Number by a Whole Number.
● Multiplication of a Fraction by Fraction.
● Properties of Multiplication of Fractional Numbers.
● Worksheet on Multiplication on Fraction.
● Division of a Fraction by a Whole Number.
● Division of a Fractional Number.
● Division of a Whole Number by a Fraction.
● Properties of Fractional Division.
● Worksheet on Division of Fractions.
● Simplification of Fractions.
● Worksheet on Simplification of Fractions.
● Worksheet on Word Problems on Fractions.
5th Grade Numbers Page
5th Grade Math Problems
From Simplification of Fractions to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Word Problems on Area and Perimeter | Free Worksheet with Answers
Jul 26, 24 04:58 PM
word problems on area and perimeter -
Worksheet on Perimeter | Perimeter of Squares and Rectangle | Answers
Jul 26, 24 04:37 PM
Practice the questions given in the worksheet on perimeter. The questions are based on finding the perimeter of the triangle, perimeter of the square, perimeter of rectangle and word problems. I. Find… -
Perimeter and Area of Irregular Figures | Solved Example Problems
Jul 26, 24 02:20 PM
Here we will get the ideas how to solve the problems on finding the perimeter and area of irregular figures. The figure PQRSTU is a hexagon. PS is a diagonal and QY, RO, TX and UZ are the respective d… -
Perimeter and Area of Plane Figures | Definition of Perimeter and Area
Jul 26, 24 11:50 AM
A plane figure is made of line segments or arcs of curves in a plane. It is a closed figure if the figure begins and ends at the same point. We are familiar with plane figures like squares, rectangles… -
5th Grade Math Problems | Table of Contents | Worksheets |Free Answers
Jul 26, 24 01:35 AM
In 5th grade math problems you will get all types of examples on different topics along with the solutions. Keeping in mind the mental level of child in Grade 5, every efforts has been made to introdu…
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.