Similar Triangles
We will discuss here about the similar triangles.
If two triangles are similar then their corresponding angles are equal and corresponding sides are proportional.
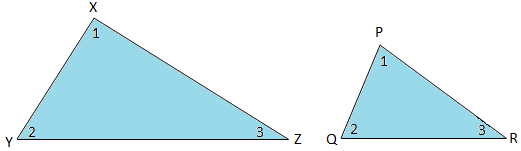
Here, the two triangles XYZ and PQR are similar.
So, ∠X = ∠P, ∠Y = ∠Q, ∠Z = ∠R and XYPQ = YZQR = XZPR.
∆XYZ is similar to ∆PQR. We write ∆XYZ ∼ ∆PQR (the symbol ‘∼’ means ‘similar to‘.)
Corrosponding Sides:
Sides opposite to equal angles in similar triangles are known as corresponding sides and they are proportional.
Here from the given figures ∠X = ∠P, ∠Y = ∠Q and ∠Z = ∠R.
Therefore, XY and PQ are corresponding sides as they are opposite to ∠Z and ∠R respectively.
Similarly from the given figure, YZ and QR are a pair of corresponding sides. XZ and PR are also a pair of corresponding sides.
Thus, XYPQ = YZQR = XZPR, as corresponding sides of similar triangles are proportional.
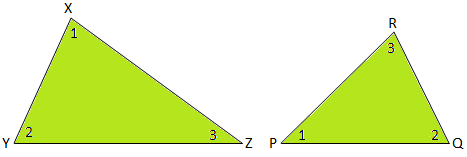
Corrosponding Angles:
Angles opposite to proportional sides in similar triangles are known as corresponding angles.
If ∆XYZ ∼ ∆PQR and XYPQ = YZQR = XZPR then ∠X = ∠P as they are opposite to corresponding sides YZ and QR respectively.
Similarly from the given figure, ∠Y = ∠Q and ∠Z = ∠R.
Congruency and Similarity of Triangles:
Congruency is a particular case of similarity. In both the cases, three angles of one triangle are equal to the three corresponding angles of the other triangle. But in similar triangles the corresponding sides are proportional, while in congruent triangles the corresponding sides are equal.
∆XYZ ∼ ∆TUV.
Therefore, XYTU = YZUV = XZTV = k, where k is the constant of proportionality or the scale factor of size transformation.
∆XYZ ≅ ∆PQR.
Here, XYPQ = YZQR = XZPR = 1.
Therefore, in congruent triangles the constant of proportionality between the corresponding sides is equal to one. Thus, congruent triangles have the same shape and size while similar triangles have the same shape but not necessarily the same size.
Congruent triangles are always similar, but similar triangles are not necessarily congruent.
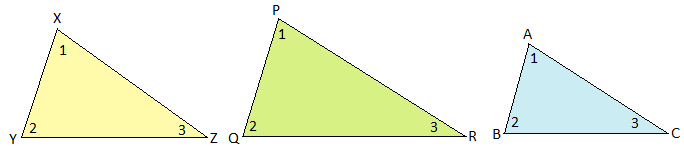
Note: Triangles that are similar to the same triangle are similar to each other.
Here, ∆XYZ ∼ ∆PQR and ∆ABC ∼ ∆PQR.
Therefore, ∆XYZ ∼ ∆ABC.
From Similar Triangles to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Vertical Subtraction | Examples | Word Problems| Video |Column Method
Mar 22, 25 05:20 PM
Vertical subtraction of 1-digit number are done by arranging the numbers column wise i.e., one number under the other number. How to subtract 1-digit number vertically? -
Worksheet on 11 Times Table | Printable Multiplication Table | Video
Mar 22, 25 05:08 PM
Worksheet on 11 times table can be printed out. Homeschoolers can also use these multiplication table sheets to practice at home. -
Worksheet on 10 Times Table | Printable Multiplication Table | Video
Mar 21, 25 03:46 PM
Worksheet on 10 times table can be printed out. Homeschoolers can also use these multiplication table sheets to practice at home. -
5th Grade Prime and Composite Numbers | Definitions | Examples | Math
Mar 21, 25 12:18 AM
5th grade prime and composite numbers -
14 Times Table | Read and Write Multiplication Table of 14| Video
Mar 20, 25 04:03 PM
In 14 times table we will learn how to read and write multiplication table of 14. We read fourteen times table as:One time fourteen is 14 Two times fourteen are 28 Three times fourteen are 42





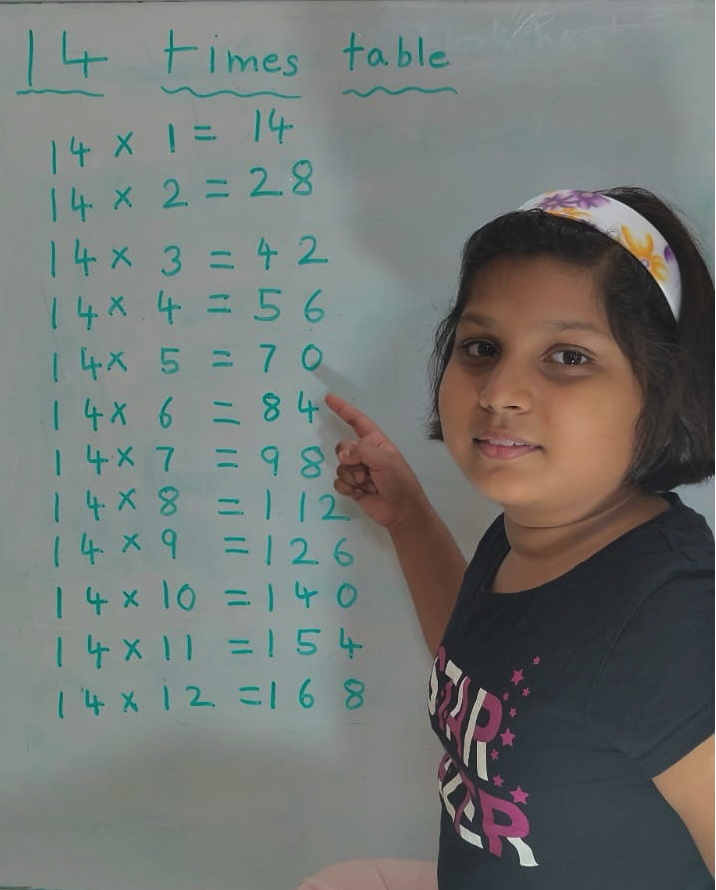
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.