Subscribe to our YouTube channel for the latest videos, updates, and tips.
Side Side Side Congruence
Conditions for the SSS - Side Side Side congruence
Two triangles are said to be congruent if three sides of one triangle are respectively equal to the three sides of the other triangle.
Experiment to prove Congruence with SSS:
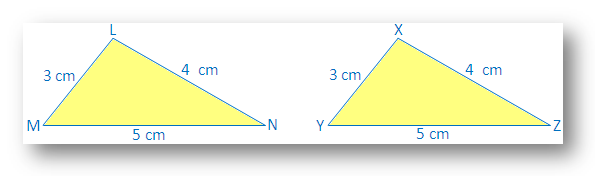
Draw ∆LMN with LM = 3 cm, LN = 4 cm, MN = 5 cm.
Also, draw another ∆XYZ with XY = 3cm, XZ = 4cm, YZ= 5cm.
We see that LM = XY, LN = XZ and MN = YZ.
Make a trace copy of ∆XYZ and try to make it cover ∆LMN with X on L, Y on M and Z on N.
We observe that: two triangles cover each other exactly.
Therefore ∆LMN ≅ ∆XYZ
Worked-out problems on side side side congruence triangles (SSS postulate):
1. LM = NO and LO = MN. Show that ∆ LON ≅ ∆ NML.
Solution:
In ∆LON and ∆NML
LM = NO → given
LO = MN → given
LN = NL → common
Therefore, ∆ LON ≅ ∆ NML, by side-side-side (SSS) congruence condition
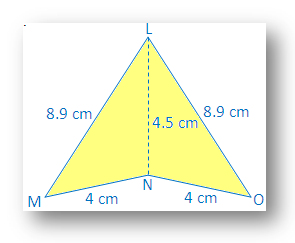
2. In the given figure, apply SSS congruence condition and state the result in the symbolic form.
Solution:
In ∆LMN and ∆LON
LM = LO = 8.9cm
MN = NO = 4cm
LN = NL = 4.5 cm
Therefore, ∆LMN ≅ ∆LON, by side side side (SSS) congruence condition
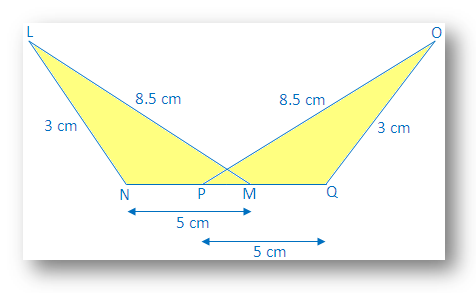
3. In the adjoining figure, apply S-S-S congruence condition and state the result in the symbolic form.
Solution:
In ∆LNM and ∆OQP
LN = OQ = 3 cm
NM = PQ = 5cm
LM = PO = 8.5cm
Therefore, ∆LNM ≅ ∆OQP, by Side Side Side (SSS) congruence condition
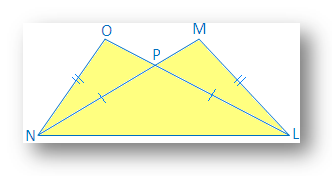
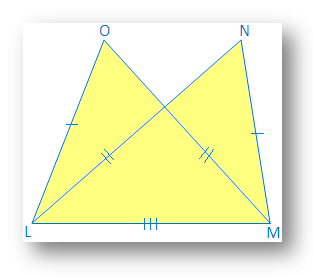
4. ∆OLM and ∆NML have common base LM, LO = MN and OM = NL. Which of the following are true?
(i) ∆LMN ≅ ∆LMO
(ii) ∆LMO ≅ ∆LNM
(iii) ∆LMO ≅ ∆MLN
Solution:
LO = MN and OM = NL → given
LM = LM → common
Thus, ∆MLN ≅ ∆LMO, by SSS congruence condition
Therefore, statement (iii) is true. So, (i) and (ii) statements are false.
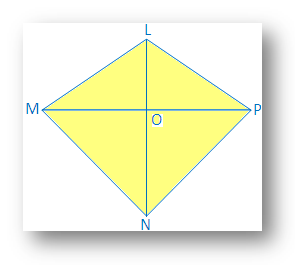
5. By Side Side Side congruence prove that 'Diagonal of the rhombus bisects each other at right angles'.
Solution: Diagonal LN and MP of the rhombus LMNP intersect each other at O.
It is required to prove that LM ⊥ NP and LO = ON and MO = OP.
Proof: LMNP is a rhombus.
Therefore, LMNP is a parallelogram.
Therefore, LO = ON and MO = OP.
In ∆LOP and ∆LOM; LP = LM, [Since, sides of a rhombus are equal]
Side LO is common
PO = OM, [Since diagonal of a parallelogram bisects each other]
Therefore, ∆LOP ≅ ∆LOM, [by SSS congruence condition]
But, ∠LOP + ∠MOL = 2 rt. angle
Therefore, 2∠LOP = 2 rt. angle
or, ∠LOP = 1 rt. angle
Therefore, LO ⊥ MP
i.e., LN ⊥ MP (Proved)
[Note: Diagonals of a square are perpendicular to each other]
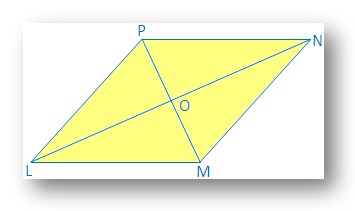
6. In a quadrilateral LMNP, LM = LP and MN = NP.
Prove that LN ⊥ MP and MO = OP [O is the point of intersection of MP and LN]
Proof:
In ∆LMN and ∆LPN,
LM = LP,
MN = NP,
LN = NL
Therefore, ∆LMN ≅ ∆LPN, [by SSS congruence condition]
Therefore, ∠MLN = ∠PLN -------- (i)
Now in ∆LMO and ∆LPO,
LM = LP;
LO is common and
∠MLO = ∠PLO
∆LMO ≅ ∆LPO, [by SAS congruence condition]
Therefore, ∠LOM = ∠LOP and
MO = OP, [Proved]
But ∠LOM + ∠LOP = 2 rt. angles.
Therefore, ∠LOM = ∠LOP = 1 rt. angles.
Therefore, LO ⊥ MP
i.e., LN ⊥ MP, [Proved]
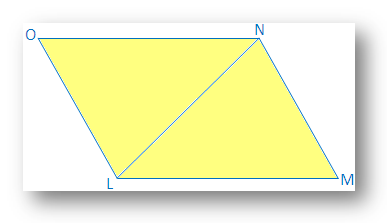
7. If the opposite sides of a quadrilateral are equal, prove that the quadrilateral will be parallelogram.
LMNO is a parallelogram quadrilateral, whose sides LM = ON and LO = MN. It is required to prove that LMNO is a parallelogram.
Construction: Diagonal LN is drawn.
Proof: In ∆LMN and ∆NOL,
LM = ON and MN = LO, [By hypothesis]
LN is common side.
Therefore, ∆LMN ≅ ∆NOL, [by Side Side Side congruence condition]
Therefore, ∠MLN = ∠LNO, [Corresponding angles of congruent triangles]
Since, LN cuts LM and ON and the both alternate angles are equal.
Therefore, LM ∥ ON
Again, ∠MNL = ∠OLN [Corresponding angles of congruent triangles]
But LN cuts LO and MN, and the alternate angles are equal.
Therefore, LO ∥ MN
Therefore, In quadrilateral LMNO,
LM ∥ ON and
LO ∥ MN.
Therefore, LMNO is a parallelogram. [Proved]
[Note: Rhombus is parallelogram.]
Conditions for the Congruence of Triangles
Right Angle Hypotenuse Side congruence
Converse of Pythagorean Theorem
7th Grade Math Problems
8th Grade Math Practice
From Side Side Side Congruence to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Terms Related to Simple Interest | Simple Interest Formula | Principal
Jun 19, 25 12:20 AM
In terms related to simple interest we will learn all the terms related to simple interest. The terms related to simple interest are Interest, Principal, Amount, Simple Interest, Time or period of tim… -
Introduction to Simple Interest | Definition | Formula | Examples
Jun 18, 25 01:50 AM
In simple interest we will learn and identify about the terms like Principal, Time, Rate, Amount, etc. PRINCIPAL (P): The money you deposit or put in the bank is called the PRINCIPAL. -
5th Grade Profit and Loss Percentage Worksheet | Profit and Loss | Ans
Jun 18, 25 01:33 AM
In 5th grade profit and loss percentage worksheet you will get different types of problems on finding the profit or loss percentage when cost price and selling price are given, finding the selling pri… -
Worksheet on Profit and Loss | Word Problem on Profit and Loss | Math
Jun 18, 25 01:29 AM
In worksheet on profit and loss, we can see below there are some different types of questions which we can practice in our homework. -
Calculating Profit Percent and Loss Percent | Profit and Loss Formulas
Jun 15, 25 04:06 PM
In calculating profit percent and loss percent we will learn about the basic concepts of profit and loss. We will recall facts and formula while calculating profit percent and loss percent. Now we wil
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.