Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
Representation of Rational Numbers on Number Line
Rational numbers can be easily represented on number line by just following some simple steps. Representation on number line depends upon the type of rational fraction is to be represented on the line. But before going to the number line don’t forget to check for the negative and positive sign of the rational number. Positive rational numbers are always represented on the right side of the zero on the number line. While negative rational numbers are always represented on the left side of zero on the number line.
Below are some of the types of rational numbers and ways to represent them on the number line:
I. Proper fraction:
We know that proper fractions are those in which numerator is less than the denominator. Such fractions exist between only zero and on. Proper fractions are less than one and greater than zero. So, proper fractions always exist between zero and one on number line. For understanding the fact more clearly let us have a look at the below given some of the examples:
1. Represent \(\frac{3}{4}\) on the number line.
Solution:
Since the given rational number is greater than zero. So, it will always be represented on the right side of zero on the number line. So, first of all we need to divide the number line between zero and one into 4 equal parts and the third part of the four parts will be representation of \(\frac{3}{4}\) on number line. It can be represented as:
2. Represent \(\frac{4}{5}\) on the number line.
Solution:
As we know that \(\frac{4}{5}\) is a positive and that too proper fraction, so it will lie at the right side of the zero and will be less than 1. To do so first we will divide number line between zero and one into 5 equal parts. \(\frac{4}{5}\)will be the fourth part of five equal parts. Let us represent this on the number line:
3. Represent \(\frac{-3}{5}\)on the number line.
Solution:
As we can see that the given fraction is a proper fraction bur with a negative sign. So, it will be smaller than zero but greater than -1. Hence, the fraction will lie between zero and negative one. To represent we will divide number line between 0 and -1 into 5 equal parts and the third part of the five parts will be \(\frac{-3}{5}\). This can be represented as:
All proper fractions can be represented on the number using above mentioned steps.
II. Improper fractions:
We know that improper fractions are those in which numerator of the fraction will be greater than its denominator. Since, the numerator is greater than the denominator the number will be greater than one. To, represent such rational fractions on the number line first we convert the improper fraction into the mixed fraction so as to know between which integers will the fraction lie.
To know the concept more clearly let us have a look at some of the examples given below:
1. Represent \(\frac{9}{5}\) on the number line.
Solution:
Since the given fraction is an improper fraction and is positive. So, it will lie on the right side of the number line. Let us first convert the given rational fraction into mixed fraction to find between which whole numbers the fraction exists on the number line. The mixed fraction conversion of the rational fraction will be 1 \(\frac{4}{5}\).,which means that the fraction would be between 1 and 2 at \(\frac{4}{5}\) point. To do so first we’ll divide number line between 1 and 2 into 5 equal parts and then the fourth part of 5 parts will be the required rational number on the number line. This can be represented as:
2. Represent \(\frac{-4}{3}\) on the number line.
Solution:
Since the given fraction is negative and is an improper fraction, so, it will lie on the left side of the zero on the number line and before we need to convert it into mixed fraction. The mixed fraction conversion of the given improper fraction is -1 \(\frac{1}{3}\).
So, the fraction will lie between -1 and -2. To represent it we will divide the number line between -1 and -2 into three equal parts and the first part of the three parts will be the required rational fraction. This can be represented as:
All improper fractions can be represented on the number using above mentioned steps.
Rational Numbers
Decimal Representation of Rational Numbers
Rational Numbers in Terminating and Non-Terminating Decimals
Recurring Decimals as Rational Numbers
Laws of Algebra for Rational Numbers
Comparison between Two Rational Numbers
Rational Numbers Between Two Unequal Rational Numbers
Representation of Rational Numbers on Number Line
Problems on Rational numbers as Decimal Numbers
Problems Based On Recurring Decimals as Rational Numbers
Problems on Comparison Between Rational Numbers
Problems on Representation of Rational Numbers on Number Line
Worksheet on Comparison between Rational Numbers
Worksheet on Representation of Rational Numbers on the Number Line
From Representation of Rational Numbers on Number Line to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
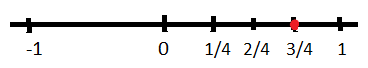
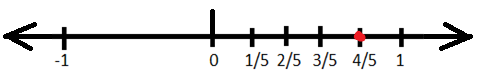
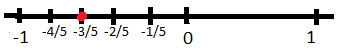
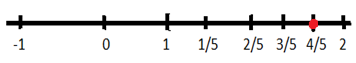



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.