Quadrilateral form a Parallelogram

Statement of the Theorem: Prove that the lines joining the middle points of the adjacent sides of a quadrilateral form a parallelogram.

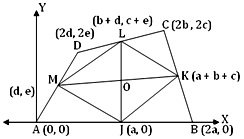
Proof: Let ABCD be a quadrilateral and length of its side AB is 2a.

Let us choose origin of rectangular cartesian co-ordinates at the vertex A and x-axis along the side AB and AY as the y-axis. Then, the co-ordinates of A and B are (0, 0) and (2a, 0) respectively. Referred to the chosen axes, let (2b, 2c) and (2d, 2e) be the co-ordinates of the vertices C and D respectively. If J, K, L, M be the mid-points of the sides AB, BC, CD, and, DA, respectively, then the co-ordinates of J, K, L and M are (a, 0 ), (a + b, c), (b + d, c + e) and (d, e) respectively. 

Now, the co-ordinates of the mid-point of the diagonal JL of the quadrilateral JKLM are {(a + b + d)/2, (c + e)/2}

Again, the co-ordinates of the mid-point of the diagonal MK of the same quadrilateral are {(a + b + d)/2, (c + e)/2}.

Clearly, the diagonals JL and MK of the quadrilateral JKLM bisect each other at ((a + b + d)/2, (c + e)/2). Hence, the quadrilateral JKLM is a parallelogram. Proved. 

● Co-ordinate Geometry 

• What is Co-ordinate Geometry?
  
• Rectangular Cartesian Co-ordinates
  
• Polar Co-ordinates
  
• Relation between Cartesian and Polar Co-Ordinates
  
• Distance between Two given Points
  
• Distance between Two Points in Polar Co-ordinates
  
• Division of Line Segment: Internal & External
  
• Area of the Triangle Formed by Three co-ordinate Points
  
• Condition of Collinearity of Three Points
  
• Medians of a Triangle are Concurrent
  
• Apollonius' Theorem
  
• Quadrilateral form a Parallelogram 
  
• Problems on Distance Between Two Points 
  
• Area of a Triangle Given 3 Points
  
• Worksheet on Quadrants
  
• Worksheet on Rectangular – Polar Conversion
  
• Worksheet on Line-Segment Joining the Points
  
• Worksheet on Distance Between Two Points
  
• Worksheet on Distance Between the Polar Co-ordinates
  
• Worksheet on Finding Mid-Point
  
• Worksheet on Division of Line-Segment
  
• Worksheet on Centroid of a Triangle
  
• Worksheet on Area of Co-ordinate Triangle
  
• Worksheet on Collinear Triangle
  
• Worksheet on Area of Polygon
  
• Worksheet on Cartesian Triangle

11 and 12 Grade Math 

From Quadrilateral form a Parallelogram to HOME PAGE