Problems on Understanding Matrices

Here we will solve different types of Problems on understanding matrices.

1. Let A = \(\begin{bmatrix} a & b\\ x & y \end{bmatrix}\). Answer the following.

(i) What is the order of the matrix A?

(ii) Find (2, 1)th and (1, 2)th elements.

Solution:

(i) The order is 2 × 2 because there are 2 rows and 2 columns in the matrix.

(ii) (2, 1)th element = the number falling in the 2^nd row and the 1^st column = x.

     (1, 2)th element = the number falling in the 1^st row and the 2^nd column = b.

2. If a matrix has eight elements, find the possible orders of the matrix.

Solution:

8 = 8 × 1, 8 = 1 × 8, 8 = 2 × 4, 8 = 4 × 2.

Therefore, the possible orders of the matrix are 8 × 1, 1 × 8, 2 × 4 and 4 × 2.

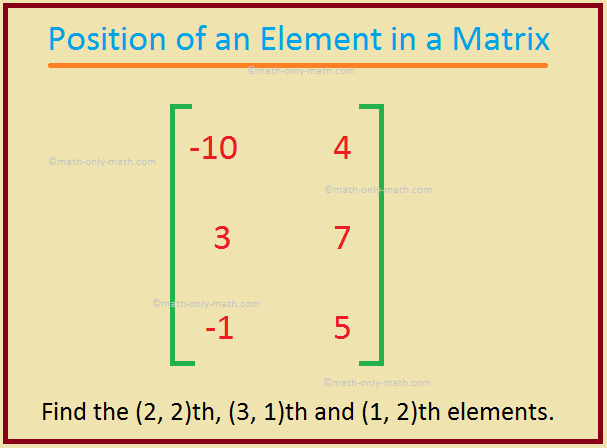
3. In the matrix \(\begin{bmatrix} -10 & 4\\ 3 & 7\\ -1 & 5 \end{bmatrix}\), find the (2, 2)th, (3, 1)th and (1, 2)th elements.

Solution:

(2, 2)th element = the number falling in the 2^nd row and the 2^nd column = 7.

(3, 1)th element = the number falling in the 3^rd row and the 1^st column = -1.

(1, 2)th element = the number falling in the 1^st row and the  2^nd column = 4.

4. If A = B, where A = \(\begin{bmatrix} 3 & x + y\\ x - y & 5 \end{bmatrix}\) and B = \(\begin{bmatrix} 3 & -7\\ 2  & 5 \end{bmatrix}\) then find x and y.

Solution:

As A = B, the corresponding elements are equal. So, x + y = -7 and x – y = 2.

Adding the two equations we get, 2x = - 5.

Therefore, x = -\(\frac{5}{2}\).

Again, subtracting the 2^nd equation from the 1^st equation we get, 2y = -9.

Therefore, y = -\(\frac{9}{2}\).

10th Grade Math

From Problems on Understanding Matrices to HOME

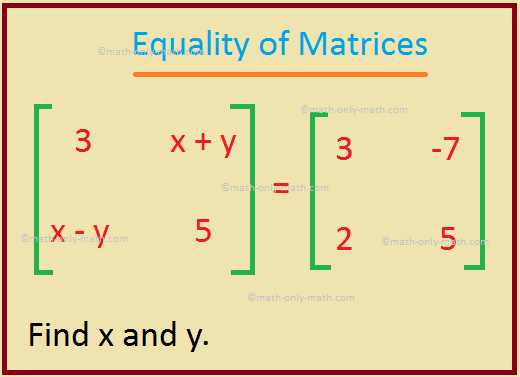
New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.

Share this page: What’s this?

FacebookXPinterestWhatsAppReddit

ShareFacebookXPinterestWhatsAppReddit