Problems on Properties of Isosceles Triangles

Here we will solve some numerical problems on the properties of isosceles triangles.

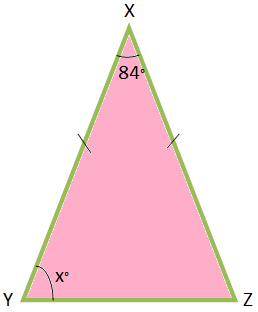
1. Find x° from the below figures.

Solution: 

In ∆XYZ, XY = XZ.

Therefore, ∠XYZ = ∠XZY = x°.

Now, ∠YXZ + ∠XYZ + XZY = 180°

⟹ 84° + x° + x° = 180°

⟹ 2x° = 180° - 84°

⟹ 2x° = 96°

⟹ x° = 48°

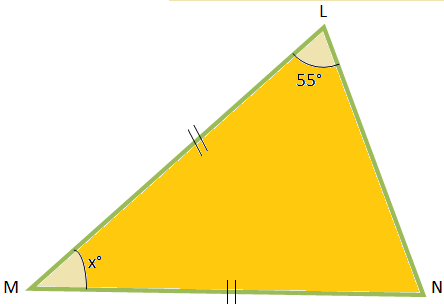
2. Find x° from the given figures.

Solution: 

LMN, LM = MN.

Therefore, ∠MLN = ∠MNL

Thus, ∠MLN = ∠MNL = 55°, [since ∠MLN = 55°]

Now, ∠MLN + ∠LMN + ∠MNL = 180°

⟹ 55° + x° + 55° = 180°

⟹ x° + 110° = 180°

⟹ x° = 180° - 110°

⟹ x° = 70°

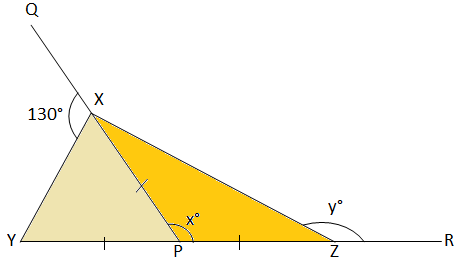
3. Find x° and y° from the given figure.

Solution:

In ∆XYP,

∠YXP = 180° - ∠QXY, as they form a linear pair.

Therefore, ∠YXP = 180° - 130°

⟹ ∠YXP = 50°

Now, XP = YP

⟹ ∠YXP = ∠XYP = 50°.

Therefore, ∠XPY = 180° - (∠YXP + ∠XYP), as the sum of three angles of a triangle is 180°

⟹ ∠XPY = 180° - (50° + 50°)

⟹ ∠XPY = 180° - 100°

⟹ ∠XPY = 80°

Now, x° = ∠XPZ = 180° - ∠XPY (linear pair).

⟹ x° = 180° - 80°

⟹ x° = 100°

Also, in ∆XPZ we have,

XP = ZP

Therefore, ∠PXZ = ∠XZP = z°

Therefore, in ∆XPZ we have,

∠XPZ + ∠PXZ + ∠XZP = 180°

⟹ x° + z° + z° = 180°

⟹ 100° + z° + z° = 180°

⟹ 100° + 2z° = 180°

⟹ 2z° = 180° - 100°

⟹ 2z° = 80°

⟹ z° = \(\frac{80°}{2}\)

⟹ z° = 40°

Therefore, y° = ∠XZR = 180° - ∠XZP

⟹ y° = 180° - 40°

⟹ y° = 140°.

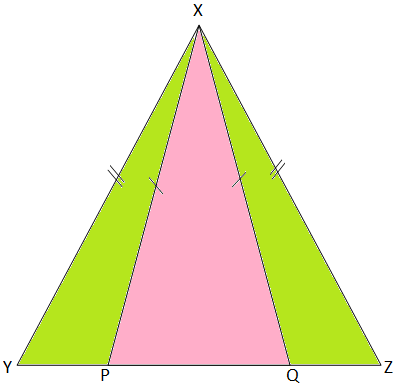
4. In the adjoining figure, it is given that XY = 3y, XZ = 7x, XP = 9x and XQ = 13 + 2y. Find the values of x and y.

Solution:

It is given that XY = XZ

Therefore, 3y = 7x

⟹ 7x - 3y = 0 ............................ (I)

Also, we have XP = XQ

Therefore, 9x = 13 + 2y

⟹ 9x – 2y – 13 = 0 ............................ (II)

Multiplying (I) by (II), we get:

14x - 6y = 0 ............................ (III)

Multiplying (II) by (III), we get:

27x – 6y – 39 = 0 ............................ (IV)

Subtracting (III) from (IV) we get,

13x - 39 = 0

⟹ 13x = 39

⟹ x = \(\frac{39}{13}\)

⟹ x = 3

Substituting x = 3 in (I) we get,

7 × 3 – 3y = 0

⟹ 21 – 3y =0

⟹ 21 = 3y

⟹ 3y = 21

⟹ y = \(\frac{21}{3}\)

⟹ y = 7.

Therefore, x = 3 and y = 7.

9th Grade Math

From Problems on Properties of Isosceles Triangles to HOME PAGE

New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.

Share this page: What’s this?

FacebookXPinterestWhatsAppReddit

ShareFacebookXPinterestWhatsAppReddit