Problems on Parallelogram

These are the various types of solved problems on parallelogram.

1. Prove that any two adjacent angles of a parallelogram are supplementary.

Solution:

Let ABCD be a parallelogram

Then, AD ∥ BC and AB is a transversal. 

Therefore, A + B = 180° [Since, sum of the interior angles on the same side of the transversal is 180°] 

Similarly, ∠B + ∠C = 180°, ∠C + ∠D = 180° and ∠D + ∠A = 180°. 

Thus, the sum of any two adjacent angles of a parallelogram is 180°. 

Hence, any two adjacent angles of a parallelogram are supplementary. 

2. Two adjacent angles of a parallelogram are as 2 : 3. Find the measure of each of its angles.

Solution:

Let ABCD be a given parallelogram

Then, ∠A and ∠B are its adjacent angles.

Let ∠A = (2x)° and ∠B = (3x)°.

Then, ∠A + ∠B = 180° [Since, sum of adjacent angles of a ∥gm is 180°]

⇒ 2x + 3x = 180

⇒ 5x = 180

⇒ x = 36.

Therefore, ∠A = (2 × 36)° = 72° and ∠B = (3 × 36°) = 108°.

Also, ∠B + ∠C = 180° [Since, ∠B and ∠C are adjacent angles]

= 108° + ∠C = 180° [Since, ∠B = 108°]

∠C = (180° - 108°) = 72°.

Also, ∠C + ∠D = 180° [Since, ∠C and ∠D are adjacent angles]

⇒ 72° + ∠D = 180°

⇒ ∠D = (180° - 72°) 108°.

Therefore, ∠A = 72°, ∠B = 108°, ∠C = 72°and ∠D = 108°.

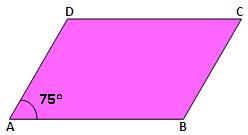
3. In the adjoining figure, ABCD is a parallelogram in which ∠A = 75°. Find the measure of each of the angles ∠B, ∠C and ∠D.

Solution:

It is given that ABCD is a parallelogram in which ∠A = 75°.

Since the sum of any two adjacent angles of a parallelogram is 180°,

∠A + ∠B = 180°

⇒ 75° + ∠B = 180°

⇒∠B = (180° - 75°) = 105°

Also, ∠B + ∠C = 180° [Since, ∠B and ∠C are adjacent angles]

⇒ 105° + ∠C = 180°

⇒ ∠C = (180° - 105°) = 75°.

Further, ∠C + ∠D = 180° [Since, ∠C and ∠D are adjacent angles]

⇒ 75° + ∠D = 180°

⇒ ∠D = (180° - 75°) = 105°.

Therefore, ∠B = 105°, ∠C = 75° and ∠D = 105°.

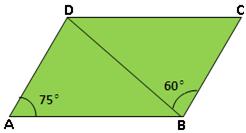
4. In the adjoining figure, ABCD is a parallelogram in which

∠BAD = 75° and ∠DBC = 60°. Calculate:

(i) ∠CDB and (ii) ∠ADB.

Solution:

We know that the opposite angles of a parallelogram are equal.

Therefore, ∠BCD = ∠BAD = 75°.

(i) Now, in ∆ BCD, we have

∠CDB + ∠DBC + ∠BCD = 180° [Since, sum of the angles of a triangle is 180°]

⇒ ∠CDB + 60° + 75° = 180°

⇒ ∠CDB + 135° = 180°

⇒ ∠CDB = (180° - 135°) = 45°.

(ii) AD ∥ BC and BD is the transversal.

Therefore, ∠ADB = ∠DBC = 60° [alternate interior angles]

Hence, ∠ADB = 60°.

`

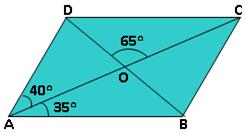
5. In the adjoining figure, ABCD is a parallelogram in which

∠CAD = 40°, ∠BAC = 35° and ∠COD = 65°.

Calculate: (i) ∠ABD (ii) ∠BDC (iii) ∠ACB (iv) ∠CBD.

Solution:

(i) ∠AOB = ∠COD = 65° (vertically opposite angles)

Now, in ∆OAB, we have:

∠OAB + ∠ABO + ∠AOB =180° [Since, sum of the angles of a triangle is 180°]

⇒ 35°+ ∠ABO + 65° = 180°

⇒ ∠ABO + 100° = 180°

⇒ ∠ABO = (180° - 100°) = 80°

⇒ ∠ABD = ∠ABO = 80°.

(ii) AB ∥ DC and BD is a transversal.

Therefore, ∠BDC = ∠ABD = 80° [alternate interior angles]

Hence, ∠BDC = 80°.

(iii) AD ∥ BC and AC is a transversal.

Therefore, ∠ACB = ∠CAD = 40° [alternate interior angles]

Hence, ∠ACB = 40°.

(iv) ∠BCD = ∠BAD = (35° + 40°) = 75° [opposite angles of a parallelogram]

Now, in ∆CBD, we have

∠BDC + ∠BCD + ∠CBD = 180° [sum of the angles of a triangle is 180°]

⇒ 80° + 75° + ∠CBD = 180°

⇒ 155° + ∠CBD = 180°

⇒ ∠CBD = (180° - 155°) = 25°.

Hence, ∠CBD = 25°.

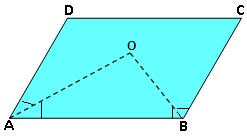
6. In the adjoining figure, ABCD is a parallelogram, AO and BO are the bisectors of ∠A and ∠B respectively. Prove that ∠AOB = 90°.

Solution:

We know that the sum of two adjacent angles of a parallelogram is 180°

Therefore, ∠A + ∠B = 180° ……………. (i)

Since AO and BO are the bisectors of ∠A and ∠B, respectively, we have

∠OAB = 1/2∠A and ∠ABO = 1/2∠B.

From ∆OAB, we have

∠OAB + ∠AOB + ∠ABO = 180° [Since, sum of the angles of a triangle is 180°]

⇒ ¹/₂∠A + ∠ABO + ¹/₂∠B = 180°

⇒ ¹/₂(∠A + ∠B) + ∠AOB = 180°

⇒ (¹/₂ × 180°) + ∠AOB = 180° [using (i)]

⇒ 90° + ∠AOB = 180°

⇒ ∠AOB = (180° - 90°) = 90°.

Hence, ∠AOB = 90°.

7. The ratio of two sides of a parallelogram is 4 : 3. If its perimeter is 56 cm, find the lengths of its sides.

Solution:

Let the lengths of two sides of the parallelogram be 4x cm and 3x cm respectively.

Then, its perimeter = 2(4x + 3x) cm = 8x + 6x = 14x cm.

Therefore, 14x = 56 ⇔ x = ⁵⁶/₁₄ = 4.

Therefore, one side = (4 × 4) cm = 16 cm and other side = (3 × 4) cm = 12 cm.

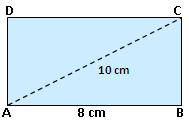
8. The length of a rectangle is 8 cm and each of its diagonals measures 10 cm. Find its breadth.

Solution:

Let ABCD be the given rectangle in which length AB = 8 cm and diagonal AC = 10 cm.

Since each angle of a rectangle is a right angle, we have

∠ABC = 90°.

From right ∆ABC, we have

AB² + BC² = AC² [Pythagoras’ Theorem]

⇒ BC² = (AC² - AB²) = {(1O)² - (8)²} = (100 - 64) = 36

⇒ BC = √36 = 6cm.

Hence, breadth = 6 cm.

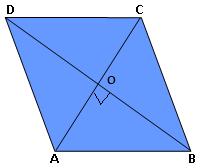
9. In the adjacent figure, ABCD is a rhombus whose diagonals AC and BD intersect at a point O. If side AB = 10cm and diagonal BD = 16 cm, find the length of diagonal AC.

Solution:

We know that the diagonals of a rhombus bisect each other at right angles

Therefore, BO = ¹/₂BD = (¹/₂ × 16) cm = 8 cm, AB = 10 cm and ∠AOB = 90°.

From right ∆OAB, we have

AB² = AO² + BO²

⇒ AO² = (AB² – BO²) = {(10) ² - (8)²} cm²

                             = (100 - 64) cm²

                             = 36 cm²

     ⇒ AO = √36 cm = 6 cm.

Therefore, AC = 2 × AO = (2 × 6) cm = 12 cm.

Parallelogram

Parallelogram

Properties of a Rectangle Rhombus and Square

Problems on Parallelogram

Practice Test on Parallelogram

Parallelogram - Worksheet

Worksheet on Parallelogram

8th Grade Math Practice

From Problems on Parallelogram to HOME PAGE