Perimeter and Area of Mixed Figures

Here we will discuss about the Perimeter and area of mixed figures.

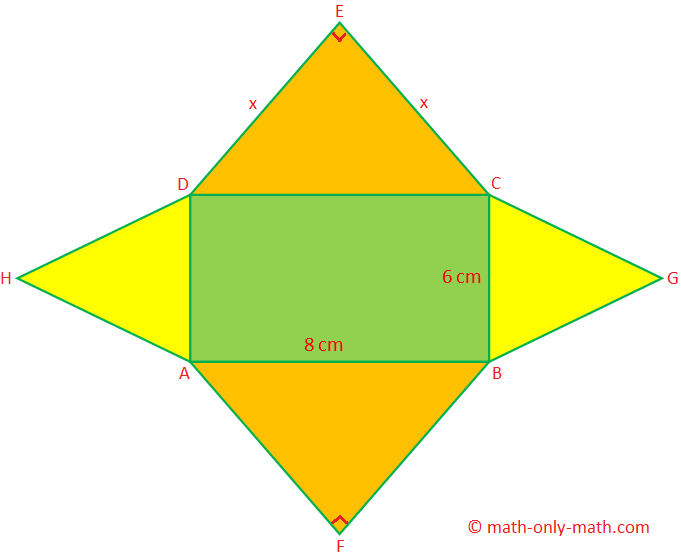
1. The length and breadth of a rectangular field is 8 cm and 6 cm respectively. On the shorter sides of the rectangular field two equilateral triangles are constructed outside. Two right-angled isosceles triangles are constructed outside the rectangular field, with the longer sides as the hypotenuses. Find the total area and perimeter of the figure.

Solution:

The figure consists of the following.

(i) The rectangular field ABCD, whose area = 8 × 6 cm$^{2}$ = 48 cm$^{2}$

(ii) Two equilateral triangles BCG and ADH. For each, area = $\frac{√3}{4}$ × 6$^{2}$ cm$^{2}$ = 9√3 cm$^{2}$

(iii) Two isosceles right-angled triangles CDE and ABF, whose areas are equal.

IF CE = ED = x then x$^{2}$ + x$^{2}$ = 8$^{2}$ cm$^{2}$ (by Pythagoras’ theorem)

or, 2x$^{2}$ = 64 cm$^{2}$

or, x$^{2}$ = 32 cm$^{2}$

Therefore, x = 4√2 cm

Therefore, area of the ∆CDE = $\frac{1}{2}$ CE × DE

                                         = $\frac{1}{2}$ x$^{2}$

                                         = $\frac{1}{2}$ (4√2)$^{2}$ cm²

                                         = $\frac{1}{2}$ 32 cm$^{2}$

                                         = 16 cm$^{2}$

Therefore, area of the figure = area of the rectangular field ABCD + 2 × area of the ∆BCG + 2 × area of the ∆CDE

                                          = (48 + 2 × 9√3 + 2 × 16) cm$^{2}$

                                          = (80 + 18√3) cm$^{2}$

                                          = (80 + 18 × 1.73) cm$^{2}$

                                          = (80 + 31.14) cm$^{2}$

                                          = 111.14 cm$^{2}$

Perimeter of the figure = length of the boundary of the figure

                                  = AF + FB + BG + GC + CE + ED + DH + HA

                                  = 4 × CE + 4 × BG

                                  = (4 × 4√2 + 4 × 6) cm

                                  = 8(3 + 2√2) cm

                                  = 8(3 + 2 × 1.41) cm

                                  = 8 × 5.82 cm

                                  = 46.56 cm

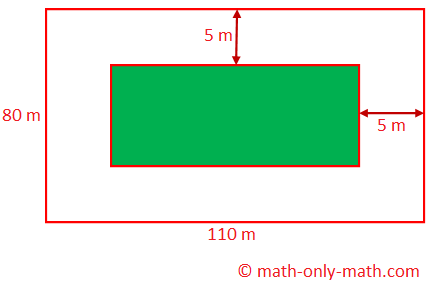
2. The dimension of a field are 110 m × 80 m. The field is to be converted into a garden, leaving a path 5 m broad around the garden. Find the total cost of making the garden if the cost per square metre is Rs 12.

Solution:

For the garden, length = (110 – 2 × 5) m = 100 m, and

                     Breadth = (80 – 2 × 5) m = 70 m

Therefore, area of the garden = 100 × 70 m$^{2}$ = 7000 m$^{2}$

Therefore, total cost of making the garden = 7000 × Rs 12 = Rs 84000

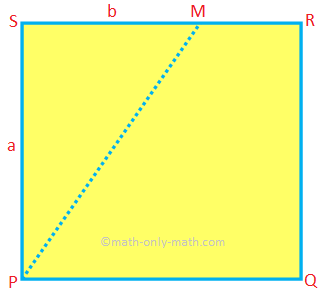
3. A square-shaped piece of paper is cut into two pieces along a line joining a corner and a point on an opposite edge. If the ratio of the areas of the two pieces be 3:1, find the ratio of the perimeters of the smaller piece and the original piece of paper.

Solution:

Let PQRS be the square-shaped piece of paper. Let its side measure a units.

It is cut along PM. Let SM = b units

Area of the ∆MSP = $\frac{1}{2}$ PS × SM = $\frac{1}{2}$ ab square units.

Area of the square PQRS = a$^{2}$ square units.

According to the question,

$\frac{\textrm{area of the quadrilateral PQRM}}{\textrm{area of the ∆MSP}}$ = $\frac{3}{1}$

⟹ $\frac{\textrm{area of the quadrilateral PQRM}}{\textrm{area of the ∆MSP}}$ + 1 = 4

⟹ $\frac{\textrm{area of the quadrilateral PQRM + area of the ∆MSP}}{\textrm{area of the ∆MSP}}$ = 4

⟹ $\frac{\textrm{area of the square PQRS}}{\textrm{area of the ∆MSP}}$ = 4

⟹ $\frac{a^{2}}{\frac{\textrm{1}}{2} ab} = 4$

⟹$\frac{2a}{b}$ = 4

⟹ a = 2b

⟹ b = $\frac{1}{2}$a

Now, PM² = PS² + SM²; (by Pythagoras’ theorem)

Therefore, PM² = a² + b²

                       = a² + ($\frac{1}{2}$a )²

                       = a² + $\frac{1}{4}$a²

                       = $\frac{5}{4}$a².

Therefore, PM² = $\frac{√5}{2}$a.

Now, $\frac{\textrm{perimeter of the ∆MSP}}{\textrm{perimeter of the square PQRS}}$ = $\frac{\textrm{MS + PS + PM}}{\textrm{4a}}$

                                         = $\frac{\frac{1}{2}a + a +\frac{\sqrt{5}}{2}a}{4a}$

                                        = $\frac{(\frac{3 + \sqrt{5}}{2})a}{4a}$

                                        = $\frac{3 + √5}{8}$

                                        = (3 + √5) : 8.

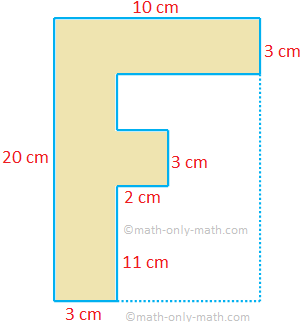
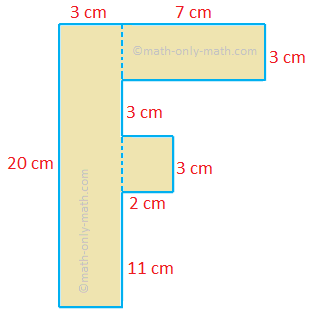
4. From a 20 cm × 10 cm plywood board an F-shaped block is cut out, as shown in the figure. What is the area of a face of the remaining board? Also find the length of the boundary of the block.

Solution:

Clearly, the block is a combination of three rectangular blocks, as shown in the below figure.

Therefore, area of a face of the block = 20 × 3 cm$^{2}$ + 3 × 2 cm$^{2}$ + 7 × 3 cm$^{2}$

                                                      = 60 cm$^{2}$ + 6 cm$^{2}$ + 21 cm$^{2}$

                                                      = 87 cm$^{2}$

Area of a face of the uncut board = 20 × 10 cm$^{2}$

                                                = 200 cm$^{2}$

Therefore, area of a face of the remaining board = 200 cm$^{2}$ - 87 cm$^{2}$

                                                                      = 113 cm$^{2}$

Required length of the boundary = (20 + 3 + 11 + 2 + 3 + 2 + 3 + 7 + 3 + 10) cm

                                               = 64 cm

9th Grade Math

From Perimeter and Area of Mixed Figures to HOME PAGE

New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.

Share this page: What’s this?

FacebookXPinterestWhatsAppReddit

ShareFacebookXPinterestWhatsAppReddit