Opposite Sides of a Parallelogram are Equal

Here we will discuss about the opposite sides of a parallelogram are equal in length.

In a parallelogram, each pair of opposite sides are of equal length.

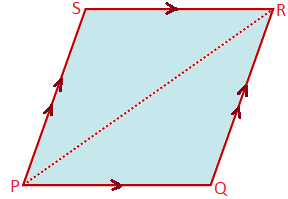
Given: PQRS is a parallelogram in which PQ ∥ SR and QR ∥ PS.

To prove: PQ = SR and PS = QR

Construction: Join PR

Proof:

Converse of the above given theorem

A quadrilateral is a parallelogram if each pair of opposite sides are equal.

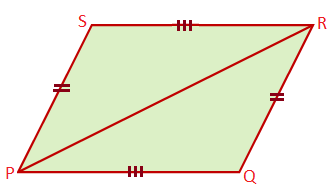
Given: PQRS is a quadrilateral in which PQ = SR and PS = QR

To prove: PQRS is a parallelogram

Proof: In ∆PQR and ∆RSP, PQ = SR, QR = SP (given) and PR is the common side.

Therefore, by SSS criterion of congruency, ∆PQR ≅ ∆RSP

Therefore, ∠QPR = ∠PRS, ∠QRP = ∠RPS  (CPCTC)

Therefore, PQ ∥ SR, QR ∥ PS

Hence, PQRS is a parallelogram.

Solved examples based on the theorem of opposite sides of a parallelogram are equal in length:

1. In the parallelogram PQRS, Pq = 6 cm and SR : RQ = 2 : 1. Find the perimeter of the parallelogram.

Solution:

In the parallelogram PQRS, PQ ∥ SR and SP ∥ RQ.

The opposite sides of a parallelogram are equal. So, SR + PQ = 6 cm.

AS SR : RQ = 23 : 1, $\frac{6 cm}{RQ}$ = $\frac{2}{1}$

⟹ RQ = 3 cm

Also, RQ = SP = 3 cm.

Therefore, perimeter = PQ + QR + RS + SP

                               = 6 cm + 3 cm + 6 cm + 3 cm

                               = 18 cm.

2. In the parallelogram ABCD, ∠ABC = 50°. Find the measures of ∠BCD, ∠CBA and ∠DAB.

Solution: 

AS AB ∥ DC, ∠ABC + ∠BCD = 180°

Therefore, ∠BCD = 180° - ∠ABC

                         = 180° - 50°

                         = 130°

As opposite angles in a parallelogram are equal, 

∠CDA = ∠ABC = 50° and

9th Grade Math

From Opposite Sides of a Parallelogram are Equal to HOME PAGE

New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.

Share this page: What’s this?

FacebookXPinterestWhatsAppReddit

ShareFacebookXPinterestWhatsAppReddit