Multiplication of Octal Numbers
In multiplication of octal numbers a simple rule for multiplication of two digits in any radix is to multiply them in decimal. If the product is less than the radix, then we take it as the result. If the product is greater than the radix we divide it by the radix and take the remainder as the least significant digit. The quotient is taken as carry in the next significant digit.
For example, (3)4 × (1)4 = (3)4 but (3)4 × (2)4 = (12)4 since 3 × 2 = 6 is decimal and division of 6 by 4 has the remainder 2 and quotient 1.
To multiply two octal numbers we use the rule given above. The process for multiplication of octal numbers is illustrated with the help of the following examples:
Evaluate:
(i) 68 × 238
Solution:
We have 6 × 3 = 18 in decimal, which when divided by 8 gives a remainder 2 and carry 2. Again 6 × 2 = 12 in decimal, and 12 + 2 = 14. This when divided by 8 gives a remainder 6 and a carry 1.
| Hence 68 × 238 = 1628 |
6 × 3 = 18 18/8 = 2 with remainder 2 → l,s,d, 6 × 2 = 12 + 2 (carry) = 14 14/8 = 1 with remainder 6. |
(ii) 158 × 448
Solution:
Since 158 = 78 + 68, We write
158 × 448 = (78 + 68) × 448 = 78 × 448 + 68 × 448
Now 7 × 44 = 374
6 × 44 = 330
Taking octal addition, we have 3748 + 3308 = 7248
Hence 158 x 448 = 7248
- Why Binary Numbers are Used
- Binary to Decimal Conversion
- Conversion of Numbers
- Hexa-decimal Number System
- Conversion of Binary Numbers to Octal or Hexa-decimal Numbers
- Octal and Hexa-Decimal Numbers
- Signed-magnitude Representation
- Radix Complement
- Diminished Radix Complement
- Arithmetic Operations of Binary Numbers
From Multiplication of Octal Numbers to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
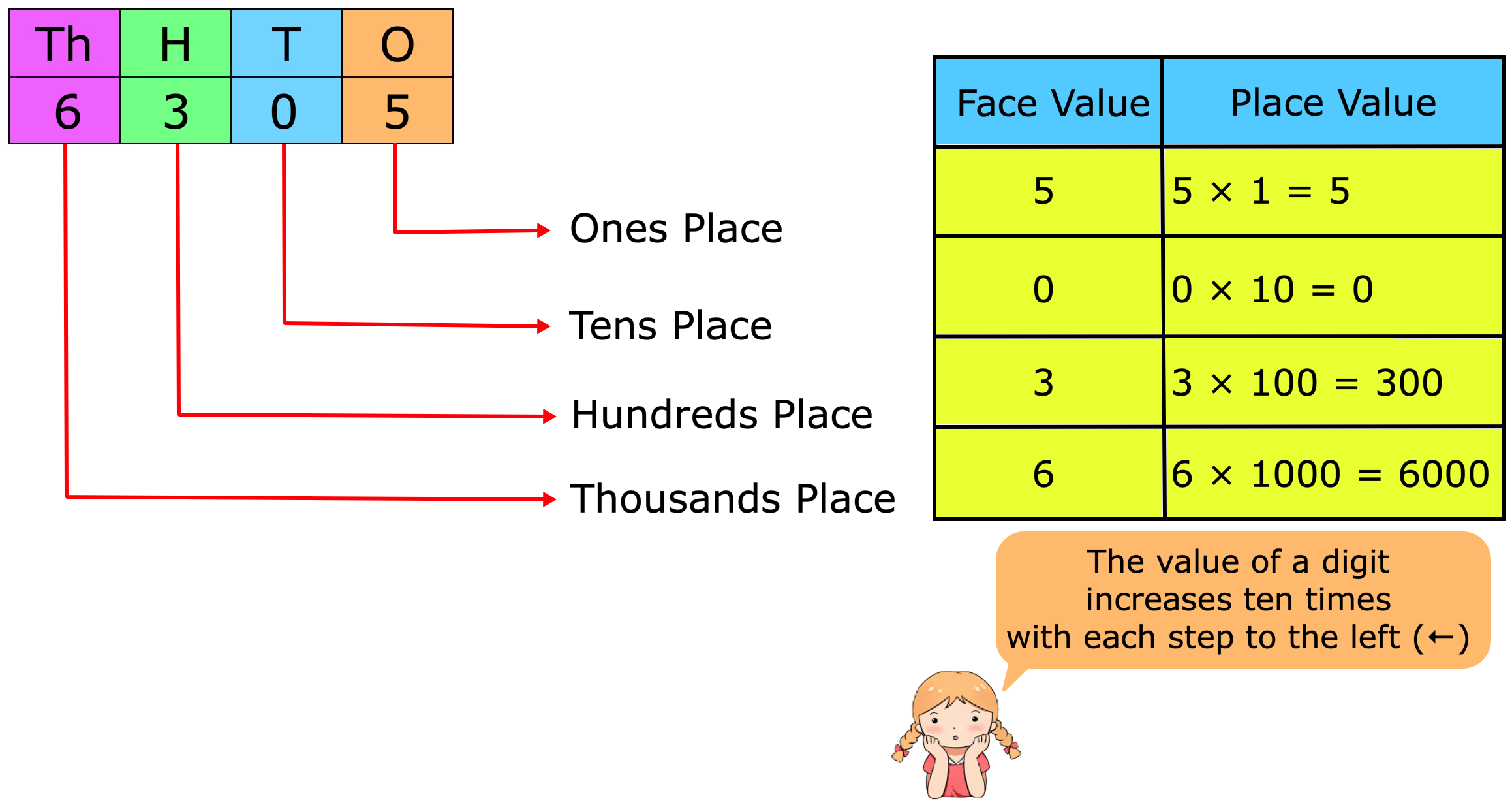
Place Value and Face Value | Place and Face Value of Larger Number
Apr 13, 25 03:12 PM
The place value of a digit in a number is the value it holds to be at the place in the number. We know about the place value and face value of a digit and we will learn about it in details. We know th… -
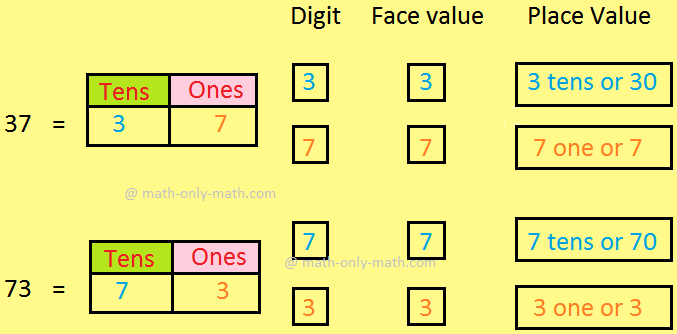
Face Value and Place Value|Difference Between Place Value & Face Value
Apr 13, 25 03:07 PM
What is the difference between face value and place value of digits? Before we proceed to face value and place value let us recall the expanded form of a number. The face value of a digit is the digit… -
Place Value and Face Value | Basic Concept on Place Value | Face Value
Apr 13, 25 02:59 PM
Learn the easiest way to understand the basic concept on place value and face value in the second grade. Suppose we write a number in figures 435 in words we write four hundred thirty five. -
Expressing Place Value and Face Value | International & Indian System
Apr 13, 25 02:35 PM
We will learn expressing place value and face value of a digit in any number in International and Indian system. Place value: We know how to find out the place value of a digit in any number. -
5th Grade Decimals | Word Problem on Decimals | Concept of Decimals
Apr 13, 25 02:16 PM
A fractional number whose denominator is 10 or multiple of 10 is called a decimal. Every decimal has two parts whole number part and decimal part. These two parts are separated by a dot or point. This…



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.