Method of Cross Multiplication

The next method of solving linear equations in two variables that we are going to learn about is method of cross multiplication.

Let us see the steps followed while soling the linear equation by method of cross multiplication:

Assume two linear equation be

 A₁ x + B₁y + C₁ = 0, and

A₂x + B₂y + C₂ = 0.

The coefficients of x are: A₁ and  A_2.

The coefficients of y are: B₁ and B_2.

The constant terms are: C₁ and  C₂.

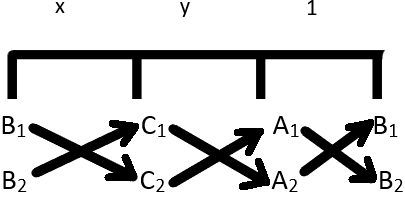
To solve the equations in a simplified way, we use following table:

$\frac{x}{B_{1}C_{2} - B_{2}C_{1}} = \frac{y}{C_{1}A_{2} - C_{2}A_{1}} = \frac{1}{A_{1}B_{2} - A_{2}B_{1}}$

Equating one another we find the value of x and y of the given equations.

Let us solve some examples based upon this concept:

1. Solve for ‘x’ and ‘y’:

 3x + 2y + 10 = 0, and

 4x + 5y + 20 = 0.

Solution:

Let us solve the given equations using method of cross multiplication:

The coefficients of x are 3 and 4.

The coefficients of y are 2 and 5.

The constant terms are 10 and 20.

The table can be formed as:

$\frac{x}{B_{1}C_{2} - B_{2}C_{1}} = \frac{y}{C_{1}A_{2} - C_{2}A_{1}} = \frac{1}{A_{1}B_{2} - A_{2}B_{1}}$

On substituting respective values, we get:

$\frac{x}{2 × 20 - 5 × 10} = \frac{y}{10 × 4 - 20 × 3} = \frac{1}{3 × 5 - 4 × 2}$

$\frac{x}{-10} = \frac{y}{-20} = \frac{1}{7}$

Equating x term with constant term, we get x = -$\frac{10}{7}$.

On equating y term with constant y term, we get y = -$\frac{20}{7}$.

2. Solve for x and y:

6x + 5y + 15 = 0, and

3x + 4y + 9 = 0.

Solution:

Let us solve the given equation using method of cross multiplication:

The coefficients of x are 6 and 3.

The coefficients of y are 5 and 4.

The constant values are 15 and 9.

The table can be formed as:

$\frac{x}{B_{1}C_{2} - B_{2}C_{1}} = \frac{y}{C_{1}A_{2} - C_{2}A_{1}} = \frac{1}{A_{1}B_{2} - A_{2}B_{1}}$

On substituting respective values, we get;

$\frac{x}{5 × 9 - 4 × 15} = \frac{y}{15 × 3 - 9 × 6} = \frac{1}{6 × 4 - 3 × 5}$

$\frac{x}{-15} = \frac{y}{-9} = \frac{1}{9}$

On equating x term with constant term, we get x= $\frac{-15}{9}$, i.e., x = -$\frac{5}{3}$.

On equating y term with constant term we get, y = $\frac{-9}{9}$

 = -1.

3. Solve for x and y:

5x + 6y + 10 = 0, and

2x + 9y = 0.

Solution:

The coefficients of x are 5 and 2.

The coefficients of y are 6 and 9.

The constant terms are 10 and 0.

The table can be formed as:

On solving, we get:

$\frac{x}{B_{1}C_{2} - B_{2}C_{1}} = \frac{y}{C_{1}A_{2} - C_{2}A_{1}} = \frac{1}{A_{1}B_{2} - A_{2}B_{1}}$

On substituting respective values, we get;

$\frac{x}{6 × 0 - 9 × 10} = \frac{y}{10 × 2 - 0 × 5} = \frac{1}{5 × 9 - 2 × 6}$

$\frac{x}{-90} = \frac{y}{20} = \frac{1}{33}$

On equating x term with constant term, we get x = $\frac{-90}{33}$ = -$\frac{30}{11}$.

On equating y term with constant term we get, y = $\frac{20}{33}$.

4. Solve for x and y;

x + y + 10 = 0.

3x + 7y + 2 = 0.

Solution:

The coefficients of x are 1 and 3.

The coefficients of y are 1 and 7.

The constant terms are 10 and 2.

The table can be formed as:

On solving this table we get,

$\frac{x}{B_{1}C_{2} - B_{2}C_{1}} = \frac{y}{C_{1}A_{2} - C_{2}A_{1}} = \frac{1}{A_{1}B_{2} - A_{2}B_{1}}$

On substituting respective values, we get;

$\frac{x}{1 × 2 - 7 × 10} = \frac{y}{10 × 3 - 2 × 1} = \frac{1}{1 × 7 - 3 × 1}$

$\frac{x}{-68} = \frac{y}{28} = \frac{1}{4}$

On equating x term with the constant term, we get; x = $\frac{-68}{4}$ = -17

On equating y term with the constant, we get; y = $\frac{28}{4}$ = 7

9th Grade Math

From Method of Cross Multiplication to HOME PAGE