Magic Square
In a magic square, every row, column and each of the diagonals add up to the same total.
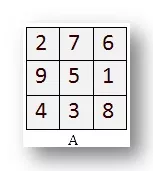
Here is a magic square. The numbers 1 to 9 are placed in the small
squares in such a way that no number is repeated and the sum of the
three digits column-wise, row-wise and diagonally is equal to 15.
This is a 3 by 3 magic square.
A. This is a magic square.
All 3 rows add upto 15.
All 3 columns add upto 15.
The 2 diagonals add upto 15.
There are 8 lines, each totaling 15.
In this magic square, numbers from 1 to 9 are used. In one of these lines, the numbers increase by 1.
The diagonal is 4, 5, 6.
Look carefully and find in which line does the numbers increase by (a) 2 (b) 3
Similar magic squares are also made.
There are the examples of magic squares formed by the numbers 5, 6, 7, 8, 9, 10, 11, 12 and 13 having the diagonally, row-wise and column-wise sum of 27
In the same pattern other magic squares may be formed.
(i) Numbers are 2, 3, 4, 5, 6, 7, 8, 9 and 10, Sum = 18
(ii) Numbers are 3 to 11 and sum = 21
(iii) Numbers are 4 to 12 and sum = 24
(iv) Numbers are 6 to 14 and sum = 30
(v) Numbers are 7 to 15 and sum = 33
(vi) Numbers are 8 to 16 and sum = 36
(vii) Numbers are 9 to 17 and sum = 39
Magic squares having 4 or more rows and columns may be made.
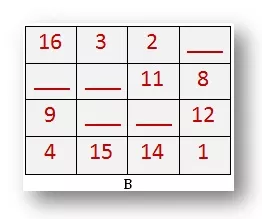
B. This is a 4 by 4 magic square. Find out the missing numbers. What does each line add up to?
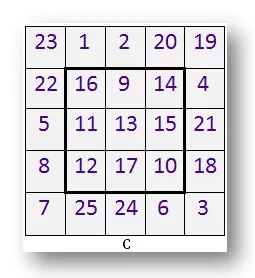
C. This is a 5 by 5 magic square.
It has 5 rows and 5 columns.
Find out the line total.
Check if each of the 5 rows, 5 columns and 2 diagonals add up to the same number.
At the centre of this 5 by 5 magic square is a 3 by 3 square. Draw this 3 by 3 square on a sheet of paper.
Copy the number in each box.
Is this 3 by 3 square A a magic square?
What is the line total of each row and column?
What is the total of the two diagonals? Do the numbers increase by 1 in any of the lines? Color that line.
Use different colors to shade lines where the numbers increase by (a) 2 (b) 3.
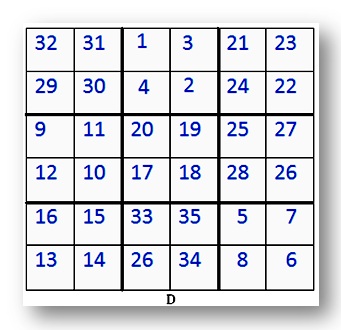
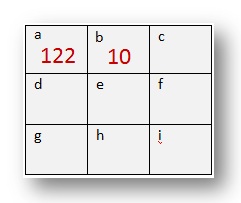
D. This is a 6 by 6 magic square.
Find the line total.
Check that some of the rows and columns add up to this number.
Notice that the thick lines divide the square into 9 smaller squares.
Each small square has 4 numbers.
What do you notice about the 4 numbers in each of this small square?
Add up the 4 numbers in each of the 9 squares.
Write your answer in a 3 by 3 square.
The first two squares haves been done for you.
(a) 29 + 30 + 31 + 32 = 122
(b) 1 + 2 + 3 + 4 = 10
(c) 21 + 22 +23 + 24 = ____
(d) 9 + 10 + 11 + 12 = ____
(e) 17 + 18 + 19 + 20 = ____
(f) 25 + 26 + 27 + 28 = ____
(g) 13 + 14 + 15 + 16 = ____
(h) 33 + 34 + 35 + 26 = ____
(i) 5 + 6 + 7 + 8 = ____
Now add up the numbers in each row, column, diagonal and confirm that this too is a magic square!
Observe the number pattern
1 ∙ 1 ∙ 2 ∙ 3 ∙ 5 ∙ 8 ∙ 13 ∙ 21 ∙ 34
Every number after the second number is equal to the sum of the two preceding numbers.
This type of relationship is called the Fibonacci sequence. It was developed by Leonardo Fibonacci of Italy around the year 1200.
We
can observe numbers from the Fibonacci sequence in various places in
nature; petals of flowers; leaves of plants; scales of pineapples and
nodes of a pine cone.
Observe the number pattern
1 ∙ 3 ∙ 6 ∙ 10 ∙ 15 ∙ 21
This number sequence is made up of triangular number.
The sequence begins with 1. Then
1 + 2 = 3
3 + 3 = 6
6 + 4 = 10
10 + 5 = 15
15 + 6 = 21
There is another interesting fact.
You can take a number of 3 digits as 356.
If we write after it the same number of three digits we get 356356.
This number is divided by 7, 11 and 13.
479479 is also divided by 7, 11 and 13.
Similarly, other numbers may be made which would be divisible by 7, 11 and 13.
Related Concept
● Patterns and Mental Mathematics
● Counting Numbers in Proper Pattern
● Puzzle
● Patterns
4th Grade Math Activities
From Magic Square to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Months of the Year | List of 12 Months of the Year |Jan, Feb, Mar, Apr
Feb 18, 25 02:20 PM
There are 12 months in a year. The months are January, February, march, April, May, June, July, August, September, October, November and December. The year begins with the January month. December is t… -
Measurement of Time | Time | Clock | Hours | Minutes | Seconds
Feb 18, 25 12:39 PM
We know that the measurement of time is read by a clock or a watch. Any clock or watch except a digital watch, has a dial. On the circular border of the dial of a watch or clock there are the -
Worksheet on Interpreting a Calendar | Questions on Calendar
Feb 18, 25 10:34 AM
In worksheet on interpreting a calendar, all grade students can practice the questions on calendar. This exercise sheet on interpreting a calendar can be practiced by the students to get more ideas to… -
Conversion of Hours into Minutes | Hours to Minutes Conversion | Time
Feb 18, 25 03:17 AM
We will discuss here about the conversion of hours into minutes. We know 1 hour is equal to 60 minutes which is required to convert the measuring time from hours to minutes. -
Reading and Interpreting a Calendar | Calendar | Reading a Calendar
Feb 18, 25 03:16 AM
In reading and interpreting a calendar we need to know days in a week, days in a month and months in a year. There are 7 days in a week. The first day of the week is Sunday.
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.