Lowest Form of a Rational Number
What is the lowest form of a rational number?
A rational number a/b is said to be in the lowest form or simplest form if a and b have no common factor other than 1.
In other words, a rational number \(\frac{a}{b}\) is said to be in the simplest form, if the HCF of a and b is 1, i.e., a and b are relatively prime.
The rational number \(\frac{3}{5}\) is in the lowest form, because 3 and 5 have no common factor other than 1. However, the rational number \(\frac{18}{60}\) is not in the lowest form, because 6 is a common factor to both numerator and denominator.
How to convert a rational number into lowest form or simplest form?
Every rational number can be put in the lowest form using the following steps:
Step I: Let us obtain the rational number \(\frac{a}{b}\).
Step II: Find the HCF of a and b.
Step III: If k = 1, then \(\frac{a}{b}\) is in lowest form.
Step IV: If k ≠ 1, then \(\frac{a ÷ k}{b ÷ k}\) is the lowest form of a/b.
The following examples will illustrate the
above procedure
to convert a rational number into lowest form.
1. Determine whether the following rational numbers are in the lowest form or not.
(i) \(\frac{13}{81}\)
Solution:
We observe that 13 and 81 have no common factor, i.e., their HCF is 1.
Therefore, \(\frac{13}{81}\) is the lowest form of a rational number.
(ii) \(\frac{72}{960}\)
Solution:
We have, 24 = 2 × 2 × 2 × 3 × 3 and 320 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 5
Thus, HCF of 72 and 960 is 2 × 2 × 2 × 3 = 24.
Therefore, \(\frac{72}{960}\) is not in the lowest form.
2. Express each of the following rational numbers to the lowest form.
(i) \(\frac{18}{30}\)
Solution:
We have,
18 = 2 × 3 × 3 and 30 = 2 × 3 × 5
Therefore, HCF of 18 and 30 is 2 × 3 = 6.
So, \(\frac{18}{30}\) is not in lowest form.
Now, dividing numerator and denominator of \(\frac{18}{30}\) by 6, we get
\(\frac{18}{30}\) = \(\frac{18 ÷ 6}{30 ÷ 6}\) = \(\frac{3}{5}\)
Therefore, \(\frac{3}{5}\) is the lowest form of a rational number \(\frac{18}{30}\).
(ii) \(\frac{-60}{72}\)
Solution:
We have
60 = 2 × 2 × 3 × 5 and 72 = 2 × 2 × 2 × 3 × 3
Therefore, HCF of 60 and 72 is 2 × 2 × 3 = 12
So, \(\frac{-60}{72}\) is not in lowest form.
Dividing numerator and denominator of \(\frac{-60}{72}\) by 12, we get
\(\frac{-60}{72}\) = \(\frac{(-60) ÷ 12}{72 ÷ 12}\) = \(\frac{-5}{6}\)
Therefore, \(\frac{-5}{6}\) is the lowest form of \(\frac{-60}{72}\).
More examples on simplest form or lowest form of a rational number:
3. Express each of the following rational numbers to the simplest form.
(i) \(\frac{-24}{-84}\)
Solution:
We have, 24 = 2 × 2 × 2 × 3 and 84 = 2 × 2 × 3 × 7
Therefore, HCF of 24 and 84 is 2 × 2 × 3 = 12
Dividing numerator and denominator of \(\frac{-24}{-84}\) by 12, we get
\(\frac{-24}{-84}\) = \(\frac{(-24) ÷ 12}{(-84) ÷ 12}\) = \(\frac{-2}{-7}\)
Therefore, \(\frac{-2}{-7}\) is the simplest form of rational number \(\frac{-24}{-84}\).
(ii) \(\frac{91}{-364}\)
Solution:
We have, 91 = 7 × 13 and 364 = 2 × 2 × 7 × 13
Therefore, HCF of 91 and 364 is 13 × 7 = 91.
Dividing numerator and denominator by 91, we get
\(\frac{91}{-364}\) = \(\frac{91 ÷ 91}{(-364) ÷ 91}\) = \(\frac{1}{-4}\)
Therefore, \(\frac{1}{-4}\) is the simplest form of \(\frac{91}{-364}\).
4. Fill in the blanks:
\(\frac{90}{165}\) = \(\frac{-6}{.....}\) = \(\frac{.....}{-55}\)
Solution:
Here, 90 = 2 × 3 × 3 × 5 and 165 = 3 x 5 x 11
Therefore, HCF of 90 and 165 is 15.
So, \(\frac{90}{165}\) is not in lowest form of rational number.
Dividing numerator and denominator by 15, we get
\(\frac{90}{165}\) = \(\frac{90 ÷ 15}{165 ÷ 15}\) = \(\frac{6}{11}\)
Thus, the rational number \(\frac{90}{165}\) in the lowest form equals \(\frac{6}{11}\)
Now, (-6) ÷ 6 = -1
Therefore, \(\frac{6}{11}\) = \(\frac{6 × (-1)}{11 × (-1)}\) = \(\frac{-6}{-11}\)
Similarly, we have (-55) ÷ 11 = -5
Therefore, \(\frac{6}{11}\) = \(\frac{6 × (-5)}{11 × (-5)}\) = \(\frac{-30}{-55}\)
Hence, \(\frac{90}{165}\) = \(\frac{-6}{-11}\) = \(\frac{-30}{-55}\)
● Rational Numbers
Introduction of Rational Numbers
Is Every Rational Number a Natural Number?
Is Every Rational Number an Integer?
Is Every Rational Number a Fraction?
Equivalent form of Rational Numbers
Rational Number in Different Forms
Properties of Rational Numbers
Lowest form of a Rational Number
Standard form of a Rational Number
Equality of Rational Numbers using Standard Form
Equality of Rational Numbers with Common Denominator
Equality of Rational Numbers using Cross Multiplication
Comparison of Rational Numbers
Rational Numbers in Ascending Order
Rational Numbers in Descending Order
Representation of Rational Numbers on the Number Line
Rational Numbers on the Number Line
Addition of Rational Number with Same Denominator
Addition of Rational Number with Different Denominator
Properties of Addition of Rational Numbers
Subtraction of Rational Number with Same Denominator
Subtraction of Rational Number with Different Denominator
Subtraction of Rational Numbers
Properties of Subtraction of Rational Numbers
Rational Expressions Involving Addition and Subtraction
Simplify Rational Expressions Involving the Sum or Difference
Multiplication of Rational Numbers
Properties of Multiplication of Rational Numbers
Rational Expressions Involving Addition, Subtraction and Multiplication
Reciprocal of a Rational Number
Rational Expressions Involving Division
Properties of Division of Rational Numbers
Rational Numbers between Two Rational Numbers
8th Grade Math Practice
From Lowest form of a Rational Number to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Worksheet on 8 Times Table | Printable Multiplication Table | Video
Mar 18, 25 03:30 PM
Worksheet on 8 times table can be printed out. Homeschoolers can also use these multiplication table sheets to practice at home. -
Worksheet on Roman Numerals |Roman Numerals|Symbols for Roman Numerals
Mar 18, 25 02:47 PM
Practice the worksheet on roman numerals or numbers. This sheet will encourage the students to practice about the symbols for roman numerals and their values. Write the number for the following: (a) V… -
Conversion of Roman Numeration | Roman Numerals |Hindu Arabic Numerals
Mar 18, 25 02:12 PM
We will learn the conversion of Roman numeration. First we will learn how to convert numbers in roman numerals. 1. Convert 579 in roman numerals. -
Rules of Roman Numeration |Roman Number System|Roman Numeration System
Mar 18, 25 09:41 AM
We will learn about Roman Numeration and its rules. We know that there are seven basic Roman Numerals. They are I, V, X, L, C, D and M. These numerals stand for the number 1, 5, 10, 50, 100, 500 -
Divisible by 2 | Test of Divisibility by 2 |Rules of Divisibility by 2
Mar 17, 25 04:04 PM
A number is divisible by 2 if the digit at unit place is either 0 or multiple of 2. So a number is divisible by 2 if digit at its units place is 0, 2, 4, 6 or 8.
● Rational Numbers - Worksheets
Worksheet on Equivalent Rational Numbers
Worksheet on Lowest form of a Rational Number
Worksheet on Standard form of a Rational Number
Worksheet on Equality of Rational Numbers
Worksheet on Comparison of Rational Numbers
Worksheet on Representation of Rational Number on a Number Line
Worksheet on Adding Rational Numbers
Worksheet on Properties of Addition of Rational Numbers
Worksheet on Subtracting Rational Numbers
Worksheet on Addition and
Subtraction of Rational Number
Worksheet on Rational Expressions Involving Sum and Difference
Worksheet on Multiplication of Rational Number
Worksheet on Properties of Multiplication of Rational Numbers
Worksheet on Division of Rational Numbers
Worksheet on Properties of Division of Rational Numbers
Worksheet on Finding Rational Numbers between Two Rational Numbers
Worksheet on Word Problems on Rational Numbers
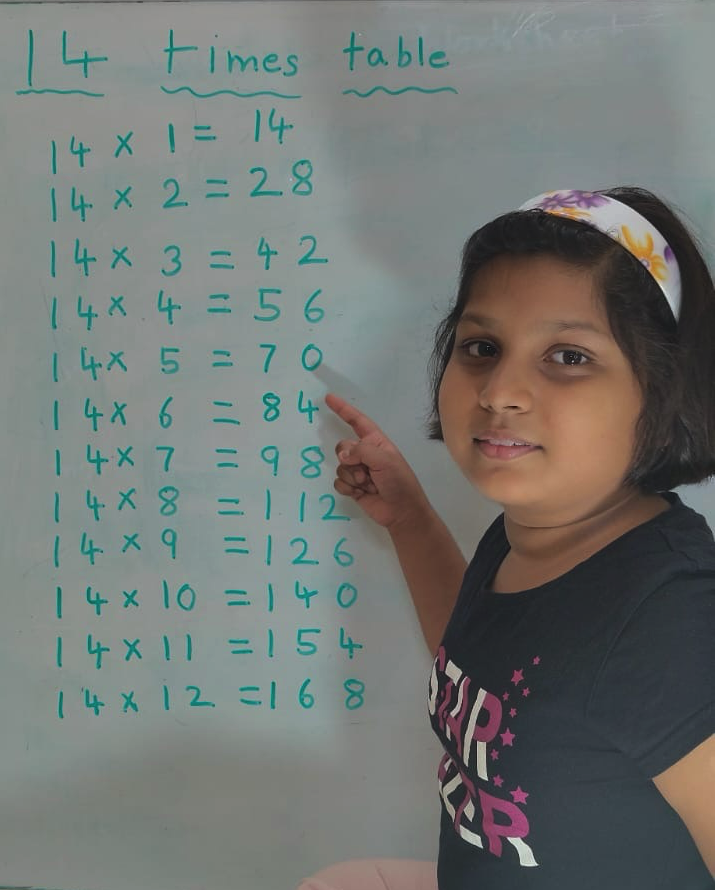
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.