Laws of Equality
Before knowing the properties of equality, let me introduce you to the properties of algebra. Below are given some properties which are applied in algebra:
1. Associative property of addition:
(a+b) +c = a + (b+c)
2. Commutative property of addition:
a + b = b + a
3. Additive property of 0:
a + 0 = 0 + a = a
4. Existence of additive inverses:
For every ‘a’ there exists (-a) so that a + (-a) = 0.
5. Associative property of multiplication:
(a x b) x c = a x (b x c)
6. Commutative property of multiplication:
a x b = b x a
7) Multiplicative identity property of 1:
a x 1 = 1 x a =a
8. Existence of multiplicative inverse:
For every ‘a’not equal to 0, there exists 1/a so that
a x 1/a = 1/a x a = 1.
9. Distributive property of multiplication over addition:
a x (b + c) = a x b + a x c
Following are the some of the solved examples based on the above given properties to make the better understanding of the concept:
1. Associative property of addition:
The way 3 numbers are grouped when adding does not change the sum.
Example: 3 + (4 + 9) = (3 + 4) + 9 = 16.
2. Commutative property of addition:
The order in which two numbers are added does not change their sum.
Example: 3 + 9 = 9 + 3 = 12.
3. Additive identity property of 0:
The sum of a number and 0 is the number itself.
Example: 16 + 0 = 0 + 16 = 16.
4. Existence of additive inverses:
The sum of a number and its compliment (opposite) is equal to 0.
Eg. 12 + (-12) = 0.
5. Associative property of multiplication:
The way 3 numbers are grouped when multiplying does not change the product.
Eg. 4 x (3 x 2) = (4 x 3) x 2 = 24.
6. Commutative property of multiplication:
The order in which two numbers are multiplied does not change their product.
Example: 4 x 8 = 8 x 4 = 32.
7. Multiplicative identity property of 1:
The product of a number and 1 is the number itself.
Example: 8 x 1 = 8
8. Existence of multiplicative inverses:
The product of a number (which is not equal to 0) and its reciprocal is equal to 1.
Example: 4 x ¼ = 1.
9. Distributive property of multiplication over addition:
When multiplying a number by a sum, the number can be multiplied by each term in the sum. Multiplication can also be distributed over subtraction.
Example: Multiplication over addition:
3 x (4 + 5) = 3 x 4 + 3 x 5 = 12 + 15 = 27.
Now, let me introduce you to the properties of equality. Following are the properties of equality:
1. Reflexive property of equality:
a = a.
2. Symmetric property of equality:
If a = b, then b = a.
3. Transitive property of equality:
If a = b and b = c, then a =c.
4. Addition property of equality;
If a = b, then a + c = b + c.
5. Subtraction property of equality:
If a = b, then a – c = b – c.
6. Multiplication property of equality:
If a = b, then a x c = b x c.
7. Division property of equality;
If a = b and ‘c’ is not equal to 0, then a/c = b/c.
8. Substitution property of equality:
If a = b, then ‘b’ may be substituted for ‘a’ in any expression containing ‘a’.
Below are given explanations and examples for the above mentioned properties of equality:
1. Reflexive property of equality:
Any number is equal to itself.
Example: 14 = 14.
2. Symmetric property of equality:
An equation may be written in the opposite order,
Example: If y = 45, then 45 = y.
3. Transitive property of equality:
Two quantities that are equal to the same thing are equal to each other.
Example: If x = 10 and 10 = y, then x = y.
4. Addition property of equality:
The same number can be added to both sides of an equation.
Example: If x = 35, then x + 4 = 35 + 4.
5. Subtraction property of equality:
The same number can be subtracted from both sides of an equation.
If x = 13, then x – 4 = 13 – 4.
6. Division property of equality:
Both sides of an equation can be divided by any non- zero number.
Example: If x = 8, then x/2 = 8/2.
7. Substitution property of equality;
A number may be substituted for its equal in any expression.
Example: If x = 80 and y = 80, then x = y.
From Laws of Equality to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Vertical Subtraction | Examples | Word Problems| Video |Column Method
Mar 22, 25 05:20 PM
Vertical subtraction of 1-digit number are done by arranging the numbers column wise i.e., one number under the other number. How to subtract 1-digit number vertically? -
Worksheet on 11 Times Table | Printable Multiplication Table | Video
Mar 22, 25 05:08 PM
Worksheet on 11 times table can be printed out. Homeschoolers can also use these multiplication table sheets to practice at home. -
Worksheet on 10 Times Table | Printable Multiplication Table | Video
Mar 21, 25 03:46 PM
Worksheet on 10 times table can be printed out. Homeschoolers can also use these multiplication table sheets to practice at home. -
5th Grade Prime and Composite Numbers | Definitions | Examples | Math
Mar 21, 25 12:18 AM
5th grade prime and composite numbers -
14 Times Table | Read and Write Multiplication Table of 14| Video
Mar 20, 25 04:03 PM
In 14 times table we will learn how to read and write multiplication table of 14. We read fourteen times table as:One time fourteen is 14 Two times fourteen are 28 Three times fourteen are 42




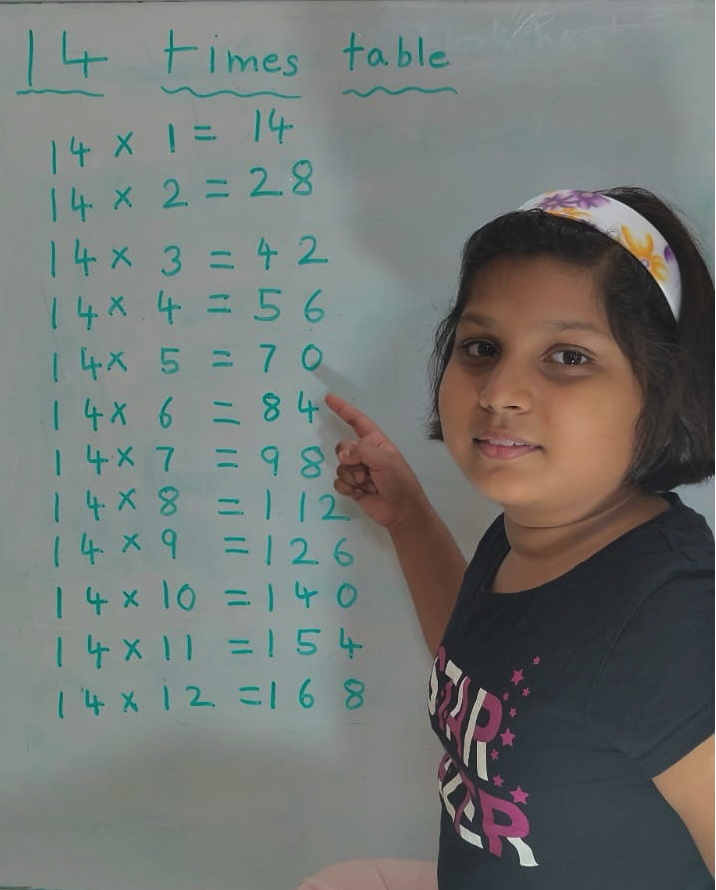
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.