Frustum of a Pyramid

If a right pyramid is cut by plane parallel to the base then the portion of the pyramid between the plane and the base of the pyramid is called a frustum of the pyramid.

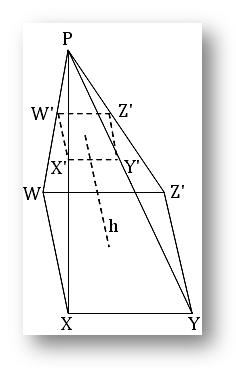
Let the square WXYZ be the base and P, the vertex of a right pyramid.

If a plane parallel to the base WXYZ of the pyramid cuts it in the plane W’X’Y’Z’ then the portion of pyramid between the planes WXYZ and W’X’Y’Z’ will be a frustum of the given pyramid. The perpendicular distance between this two planes is the height of the frustum. Clearly side-face (viz. WXX’W’, XYY’X’ ect.) are trapeziums; the distance between the parallel sides of this trapeziums is the slant height of the frustum of the pyramid.

Let S₁ and S₂ be the areas of the lower and upper planes respectively of the frustum of a pyramid; if h and l be the height and slant height respectively of the frustum, then 





(A) Area of the slant faces of the frustum 

= ½ × (perimeter of the lower face + perimeter of the upper face) × l.

(B) Area of whole surface of the frustum 

= Area of the slant faces + S₁ + S₂;

(C) Volume of the frustum = 1/3 × (S₁ + S₂ + √ S₁ S₂) × h.

Worked-out problems on Frustum of a Pyramid:

A monument has the shape of a frustum of a right pyramid whose lower and upper plane faces are squares of sides 16 meter and 9 meter respectively. If the height of the monument is 21 meter, find its volume.

Solution:

Clearly, the area of the lower faces of the monument = S₁ = (16)² square meter = 256 square meter and the area of the upper face of the monument = S₂ = 9² square meter = 81 square meter.

Therefore, the volume of the monument

= the volume of the frustum of a right pyramid

= 1/3 × (S₁ + S₂ + √S₁S₂) × height of the frustum

= 1/3 × [256 + 81 + √{(16)² × 9²} × 21 cubic meter.

= 1/3 × (256 + 81 + 144) × 21 cubic meter.

= 1/3 × 481 × 21 cubic meter.

= 7 × 481 cubic meter.

= 3367 cubic meter.

From Frustum of a Pyramid to HOME PAGE