Formulas for 3D Shapes

Some of the useful math geometry formulas for 3D shapes are discussed below.

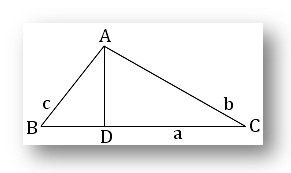
(i) Area of a Triangle: Let ABC be any triangle. If AD be perpendicular to BC and BC = a, CA = b, AB = c then the area of the triangle ABC (to be denoted by ⊿) is given by,

⊿ = ¹/₂ × base × altitude. 

= ¹/₂ ∙ BC ∙ AD 

(b) ⊿ = √[s(s - a)(s - b)(s - c)] 

Where 2x = a + b + c = perimeter of the ⊿ ABC. 

(c) If the a be the length of a side of an equilateral triangle then its height = (√3/2) a and it’s area = (√3/4) a²

(ii) If a be the length and b, the breadth of a rectangle then its area = a ∙ b, length of its diagonal = √(a² + b² ) and its perimeter = 2 ( a + b). 

(iii) If a be the length of a side of a square, then its area = a² length of its diagonal = a√2 and perimeter = 4a.


(iv) If the lengths of two diagonals of a rhombus be a and b respectively then its area = (1/2) ab and length of a side = (1/2) √(a² + b²)


(v) If a and b be the lengths of two parallel sides of a trapezium and h be the distance between the parallel sides then the area of the trapezium = (1/2) (a + b) ∙ h.


(vi) Area of a Regular Polygon: The area of a regular polygon of n sides = (na²/4) cot (π/n) where a is the length of a side of the polygon. In particular, if a be the length of a side of a regular hexagon then its area

= (6a²/4) ∙ cot (π/6) = (3√3/2) ∙ a²


(vii) The length of circumference of a circle of radius r is 2πr and
its area = πr²


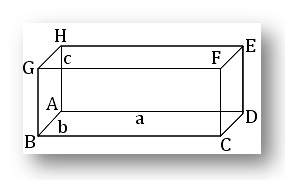
(viii) Rectangular Parallelopiped: If a, b and c be the length, breadth and height respectively of a rectangular parallelopiped then,

(a) the area of its surfaces = 2 ( ab + bc + ca) 

(b) its volume = abc and 

(c) the length of diagonal = √(a² + b² + c² ).

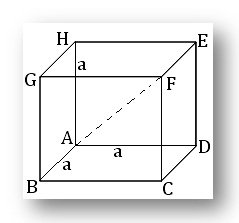
(ix) Cube: If the length of the side of a cube be a then,

(a) the area of its surfaces = 6a²,

(b) its volume = a³ and

(c) the length of the diagonal = √3a.


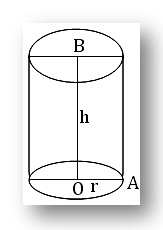
(x) Cylinder: Let r (= OA) be the radius of the base and h (=OB) be the height of a right circular cylinder ; then

(a) area of its curved surface = perimeter of base × height = 2πrh

(b) area of the whole surface = area of its curved surface + 2 × area of circular base
                                                = 2πrh + 2πr²
                                                = 2πr(h + r)

(c) volume of cylinder = area of base × height
                                    = πr²h


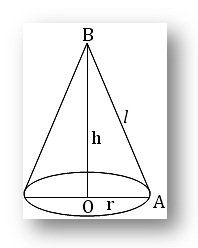
(xi) Cone: Let r (= OA) be the radius of the base, h (= OB), the height and I, the slant height of a right circular cone ; then

(a) l² = h² + r²

(b) area of its curved surface

= (1/2) × perimeter of the base × slant height = (1/2)∙ 2πr ∙ l = πrl

(c) area of its whole surface = area of the curved surface + area of the circular base

= πrl + πr² = πrl + πr(l + r).

(d) volume of the cone = (1/3) × area of the base × height = (1/3)πr²h

● Mensuration

• Formulas for 3D Shapes
  
• Volume and Surface Area of the Prism
  
• Worksheet on Volume and Surface Area of Prism
  
• Volume and Whole Surface Area of Right Pyramid
  
• Volume and Whole Surface Area of Tetrahedron
  
• Volume of a Pyramid
  
• Volume and Surface Area of a Pyramid
  
• Problems on Pyramid
  
• Worksheet on Volume and Surface Area of a Pyramid
  
• Worksheet on Volume of a Pyramid

11 and 12 Grade Math 

From Formulas for 3D Shapes to HOME PAGE