Exponents

In exponents we will mainly learn about the exponential form and product form, negative integral exponents, positive and negative rational exponents, laws of exponents etc,. To write large numbers in shorter form, so that it becomes very convenient to read, understand and compare, we use exponents. In exponents we will learn more about exponents and their uses.

When a number is multiplied with itself a number of times, then it can be expressed as a number raised to the power of a natural number, equal to the number of times the number is multiplied with itself.

For example:

3 × 3 × 3 × 3 × 3 can be written as 3⁵ and is read as 3 raised to the power 5. Here the base is 3 and the exponent is 5.

Similarly, for any rational number ’a’ and a positive integer, we define aⁿ as a × a × a × a × ………… a (n times) 

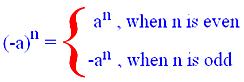
For example:

(i) (-2)⁴ = -2 × -2 × -2 × -2

(ii) (-2)³ = -2 × -2 × -2

aⁿ is called the nth power of a and can be read as:
a raised to the power n. 

The rational number a is called the base and n is called the exponent or the power or the index.

Therefore the notation of writing the product of rational number by itself several times is called the exponential notation or the power notation. Exponential notation is also known as power notation.


Examples on exponential form;

(i) We can write -5 × -5 × -5 × -5 in the exponential form as (-5)⁴ and is read as -5 raised to the power 4. Here, (-5) is the base.

(ii) Also, 3/2 × 3/2 × 3/2 × 3/2 × 3/2 in the exponential form is written as (3/2)⁵ and is read as 3/2 raised to the power 5. Here, 3/2 is the base, 5 is the exponent.



Examples on product form;

(i) We can write 5³ in the product form as 5 × 5 × 5
and its product as 125.

(ii) Similarly, (-4/3)² is written as -4/3 × -4/3 and its product is 16/9.

Powers with positive and negative exponents such as 5² or (-5)² is the positive exponent and 5\(^{-2}\) or (-5)\(^{-2}\) is the negative exponent. 

Powers with Positive Exponents

We know that 10² = 10 × 10 = 100

10 = 1

10¹ = 10

10² = 10 × 10 = 100

10³ = 10 × 10 × 10 = 1000

10⁴ = 10 × 10 × 10 × 10 = 10000

10⁵ = 10 × 10 × 10 × 10 × 10 = 100000

Powers with Negative Exponents

Powers with negative exponents is also known as negative integral exponents.

So, 10\(^{-1}\) = 1/10

10\(^{-2}\) = 1/10²

10\(^{-3}\) = \(\frac{1}{10^{3}}\)

Thus, for any non zero rational number ‘a’ and a positive integer we define.

a\(^{-n}\) = 1/aⁿ

i.e., a\(^{-n}\) is the reciprocal of aⁿ or a\(^{-n}\) is the multiplicative inverse of aⁿ

Solved examples on exponents

1. Express the following in power notation:

(i) -2/7 × -2/7 × -2/7

= (-2/7)³

(ii) -1 × -1 × -1 × -1

= (-1)⁴


(iii) 5/3 × 5/3 × 5/3 × 5/3 × 5/3 × 5/3 × 5/3

= (5/3)⁷


2. Express each of the following as rational number:

(i) (-5/7)³

= (-5/7) × (-5/7) × (-5/7)

= -125/243


(ii) (-1)⁶

= -1 × -1 × -1 × -1 × -1 × -1

= 1


(iii) (-1)³

= -1 × -1 × -1

= -1


(iv) (2/3)⁴

= 2/3 × 2/3 × 2/3 × 2/3

= 16/81



3. Express each of the following in the exponential form:

(i) 125/27

We can write 125 = 5 × 5 × 5 = 5³ and 27 = 3 × 3 × 3 = 3³

So, 125/27 = 5³/3³ = (5/3)³


(ii) -1/32

We can write -1 = (-1) × (-1) × (-1) × (-1) × (-1) = (-1)⁵

and 32 = 2 × 2 × 2 × 2 × 2 = 2⁵

So, -1/32 = (-1) ⁵/2⁵= (-1/2)⁵


(iii) 16/81

= (2 × 2 × 2 × 2)/( 3 × 3 × 3 × 3)

= 2⁴/3⁴

= (2/3)⁴


(iv) -1/64

= (-1 × -1 × -1)/(4 × 4 × 4)

= (-1/4)³



4. Express each of the following in the product form and find its value.

(i) (2/5)³

= 2/5 × 2/5 × 2/5

= 8/125


(ii) (-1/7)⁴

= -1/7 × -1/7 × -1/7 × -1/7

= 1/2401


(iii) (-8)³

= -8 × -8 × -8

= -512

● Exponents

Exponents

Laws of Exponents

Rational Exponent

Integral Exponents of a Rational Numbers

Solved Examples on Exponents

Practice Test on Exponents

● Exponents - Worksheets

Worksheet on Exponents

8th Grade Math Practice

From Exponents to HOME PAGE