Distance between Two Points

Here we will discuss about distance between two points.

How to find the distance between two given points?

Or,

How to find the length of the line segment joining two given points?

(A) To find the distance of a given point from the origin:

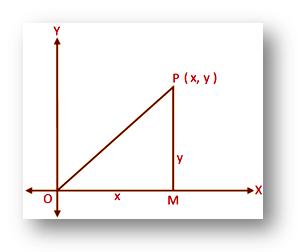
Let OX and OYbe the rectangular Cartesian Co-ordinates axes on the plane of reference and the Co-ordinates of a point P on the plane be (x, y). to find the distance of P from the origin O. from P draw PM perpendicular on OX; then , OM = x and PM = y. Now from the right angle triangle OPM we get,

OP² = OM² + PM² = x² + y²

Therefore OP = √(x² + y²) (Since, OP is positive.)

(B) To find the distance between two points whose rectangular Cartesian co-ordinates are given:

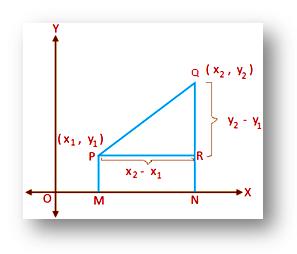
Let (x₁, y₁) and (x₂, y₂) be the Cartesian co-ordinates of the points P and Q respectively referred to rectangular co-ordinate axes OX and OY. We are to find the distance between the points P and Q. Draw PM and QN perpendiculars from P and Q respectively on OX; then draw PR perpendicular from P on QN.

Clearly, OM = x₁, PM = y₁, ON = x₂ and QN = y₂.

Now, PR = MN = ON - OM = x₂ – x₁
and QR = QN - RN = QN - PM = y₂ – y₁

Therefore, from the right-angled triangle PQR we get,

PQ² = PR² + QR² = (x₂ - x₁)² + ( y₂ - y₁)²

Therefore, PQ = √[(x₂ - x₁)² + (y₂ - y₁)²] (Since, PQ is positive )∙

Examples on Distance between two Points

1. Find the distance of the point (-5, 12) from the origin.

Solution:

We know that, the distance between two given points (x₁, y₁) and (x₂, y₂) is

√{(x₂ - x₁)² + (y₂ - y₁)²}.

The required distance of the point (- 5, 12) from the origin = the distance between the points (- 5, 12) and (0, 0)

      = √{(- 5 - 0)² + (12 - 0)²}

      = √(25 + 144)

      = √169

      = 13 units.

2. Find the distance between the points (- 2, 5) and (2, 2).

Solution:

We know that, the distance between two given points (x₁, y₁) and (x₂, y₂) is

√{(x₂ - x₁)² + (y₂ - y₁)²}.

The required distance between the given points (- 2, 5) and (2, 2)

      = √{(2 + 2)² + (2 - 5)²} 

      = √(16 + 9)

      = √25

      = 5 units.

● Co-ordinate Geometry 

• What is Co-ordinate Geometry?
  
• Rectangular Cartesian Co-ordinates
  
• Polar Co-ordinates
  
• Relation between Cartesian and Polar Co-Ordinates
  
• Distance between Two given Points
  
• Distance between Two Points in Polar Co-ordinates
  
• Division of Line Segment: Internal & External
  
• Area of the Triangle Formed by Three co-ordinate Points
  
• Condition of Collinearity of Three Points
  
• Medians of a Triangle are Concurrent
  
• Apollonius' Theorem
  
• Quadrilateral form a Parallelogram 
  
• Problems on Distance Between Two Points 
  
• Area of a Triangle Given 3 Points
  
• Worksheet on Quadrants
  
• Worksheet on Rectangular – Polar Conversion
  
• Worksheet on Line-Segment Joining the Points
  
• Worksheet on Distance Between Two Points
  
• Worksheet on Distance Between the Polar Co-ordinates
  
• Worksheet on Finding Mid-Point
  
• Worksheet on Division of Line-Segment
  
• Worksheet on Centroid of a Triangle
  
• Worksheet on Area of Co-ordinate Triangle
  
• Worksheet on Collinear Triangle
  
• Worksheet on Area of Polygon
  
• Worksheet on Cartesian Triangle

11 and 12 Grade Math 

From Distance between Two Points to HOME PAGE