Diminished Radix Complement
Diminished Radix Complement Representation:
In the decimal number system the diminished radix complement is 9’s complement. This is obtained by subtracting each digit of the number from 9.
Decimal Number59 894 6578 2063 |
9’s Complement40 105 3421 7936 |
The diminished radix complement of binary numbers is called 1’s complement. The 1’s complement of a binary number is formed by replacing each 1 in the number by a 0 and each 0 by 1.
For example, 1’s complements of some binary numbers are;
Binary Number1011 1101 |
1’s Complement0100 0010 |
In the case of signed magnitude representation of binary numbers, the MSB is the sign bit.
Positive number representations are same for both 1’s and 2’s complement. But representation of negative numbers differs by 1. A weight of -(2n-1 - 1) rather than -2n-1 is given to the MSB while computing the decimal equivalent of 1’s complement of a binary number.
A few examples of 8-bit binary numbers and their 1’s complement are given below;
Binary Number(i) 010100011’s complement 10101110 (ii) 10101000 1’s complement 01010111 |
Decimal Equivalent+81-127 + 46 = -81 -127 + 40 = -87 +87 |
- Why Binary Numbers are Used
- Binary to Decimal Conversion
- Conversion of Numbers
- Hexa-decimal Number System
- Conversion of Binary Numbers to Octal or Hexa-decimal Numbers
- Octal and Hexa-Decimal Numbers
- Signed-magnitude Representation
- Radix Complement
- Diminished Radix Complement
- Arithmetic Operations of Binary Numbers
From Diminished Radix Complement to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
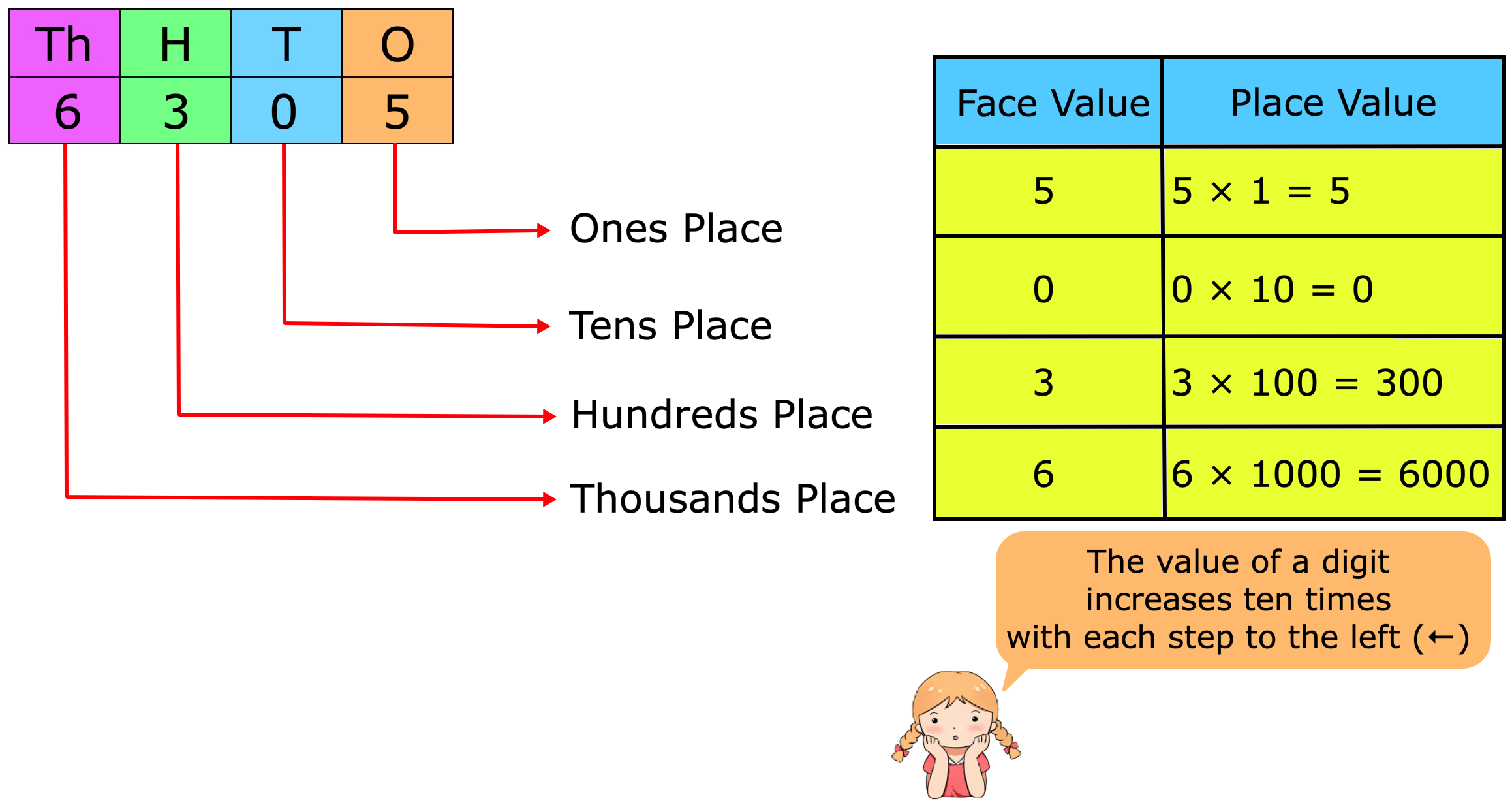
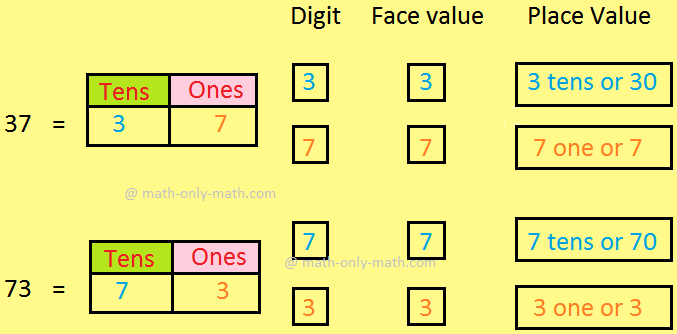
Place Value and Face Value | Place and Face Value of Larger Number
Apr 13, 25 03:12 PM
The place value of a digit in a number is the value it holds to be at the place in the number. We know about the place value and face value of a digit and we will learn about it in details. We know th… -
Face Value and Place Value|Difference Between Place Value & Face Value
Apr 13, 25 03:07 PM
What is the difference between face value and place value of digits? Before we proceed to face value and place value let us recall the expanded form of a number. The face value of a digit is the digit… -
Place Value and Face Value | Basic Concept on Place Value | Face Value
Apr 13, 25 02:59 PM
Learn the easiest way to understand the basic concept on place value and face value in the second grade. Suppose we write a number in figures 435 in words we write four hundred thirty five. -
Expressing Place Value and Face Value | International & Indian System
Apr 13, 25 02:35 PM
We will learn expressing place value and face value of a digit in any number in International and Indian system. Place value: We know how to find out the place value of a digit in any number. -
5th Grade Decimals | Word Problem on Decimals | Concept of Decimals
Apr 13, 25 02:16 PM
A fractional number whose denominator is 10 or multiple of 10 is called a decimal. Every decimal has two parts whole number part and decimal part. These two parts are separated by a dot or point. This…



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.