Cube Root

The cube root of a number is denoted by ∛

The cube root of a number x is that number whose cube gives x. We denote the cube root of x by ∛x

Thus, 3√64 = cube root of 64 = 3∛4 × 4 × 4 = ∛4³ = 4


For example:

(i) Since (2 × 2 × 2) = 8, we have ∛8 = 2

(ii) Since (5 × 5 × 5) = 125, we have ∛125 = 5

Method of finding the cube root of a given number by factorization

To find the cube root of a given number, proceed as follows:

Step I. Express the given number as the product of primes.

Step II. Make groups in triplets of the same prime.

Step III. Find the product of primes, choosing one from each triplet.

Step IV. This product is the required cube root of the given number.

Note: If the group in triplets of the same prime factors cannot complete, then the exact cube root cannot be found.

Solved Examples of Cube Root using step by step with explanation

1. Evaluate the cube root: ∛216

Solution:

By prime factorization, we have

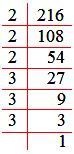
216 = 2 × 2 × 2 × 3 × 3 × 3

= (2 × 2 × 2) × (3 × 3 × 3)

Therefore, ∛216 = (2 × 3) = 6



2. Evaluate the cube root: ∛343

Solution:

By prime factorization, we have

343 = 7 × 7 × 7

= (7 × 7 × 7).

Therefore, ∛343 = 7



3. Evaluate the cube root: ∛2744

Solution:

By prime factorization, we have

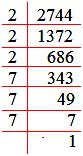
2744 = 2 × 2 × 2 × 7 × 7 × 7

= (2 × 2 × 2) × (7 × 7 × 7).

Therefore, ∛2744 = (2 × 7) = 14

Cube Root of a Negative Perfect Cube

Let (a) be a positive integer. Then, (-a) is a negative integer.

We know that (-a)³ = -a³.

Therefore, ∛-a³ = -a.

Thus, cube root of (-a³) = -(cube root of a³).

Thus, = ∛-x = - ∛x

For example:

Find the cube root of (-1000).

Solution:

We know that ∛-1000 = -∛1000

Resolving 1000 into prime factors, we get

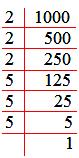
1000 = 2 × 2 × 2 × 5 × 5 × 5

= (2 × 2 × 2) × (5 × 5 × 5)

Therefore, ∛1000 = (2 × 5) = 10

Therefore, ∛-1000 = -(∛1000) = -10

Cube Root of Product of Integers:

We have, ∛ab = (∛a × ∛b).

For example: 

1. Evaluate: ∛(125 × 64).

Solution:

(∛125 × 64)

= ∛125 × ∛64

= [∛{5 × 5 × 5}] × [∛{4 × 4 × 4}]

= (5 × 4)

= 20



2. Evaluate: ∛(27 × 64).

Solution:

(∛27 × 64)

= ∛27 × ∛64

= [∛{3 × 3 × 3}] × [∛{4 × 4 × 4}]

= (3 × 4)

= 12



3. Evaluate: ∛[216 × (-343)].

Solution:

∛[216 × (-343)]

= ∛216 × ∛-343

= [∛{6 × 6 × 6}] × [∛{(-7) × (-7) × (-7)}]

= [6 × (-7)] = -42.

Cube Root of a Rational Number:

We define: ∛(a/b) = (∛a)/(∛b)

For example:

Evaluate:

{∛(216/2197)


Solution:

∛(216/2197)

= ∛216/∛2197

= [∛(6 × 6 × 6)]/[ ∛(13 × 13 × 13)]

= 6/13

Cube Root of Fractions:

Cube root of a fraction is a fraction obtained by taking the cube roots of the numerator and the denominator separately.

If a and b are two natural numbers, then ∛(a/b) = (∛a)/(∛b)

For Example:

∛(-125/512)

= ∛(-125)/∛512

= ∛{(-5) × (-5) × (-5)}/∛{8 × 8 × 8}

= -5/8

Cube Root of Decimals:

Express the given decimal in the fraction form and then find the cube root of the numerator and denominator separately and convert the same into decimal.

For Example:

Find the cube root of 5.832.

Solution:

Converting 5.832 into fraction, we get 5832/1000

Now ∛5832/1000 = ∛5832/∛1000

= ∛(2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3)/∛(2 × 2 × 2 × 5 × 5 × 5)

= 2 × 3 × 3/2 × 5

= 18/10

= 1.8

● Cube and Cube Roots

Cube

To Find if the Given Number is a Perfect Cube

Cube Root

Method for Finding the Cube of a Two-Digit Number

Table of Cube Roots

● Cube and Cube Roots - Worksheets

Worksheet on Cube

Worksheet on Cube and Cube Root

Worksheet on Cube Root

8th Grade Math Practice

From Cube Root to HOME PAGE