Coordinates of a Point in a Plane

How to determine the coordinates of a point in a plane?

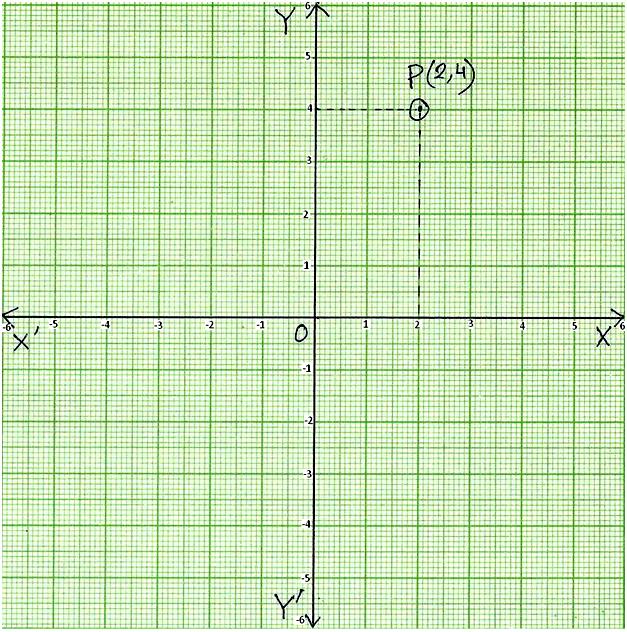
$\overrightarrow{XOX'}$ and $\overrightarrow{YOY'}$ represent the co-ordinate axes. P be a point in the plane of the graph paper.

Draw $\overline{PM}$ ┴ $\overrightarrow{YOY'}$ and $\overline{PN}$ ┴ $\overrightarrow{XOX'}$.

Length of $\overline{ON}$ is called the x- co-ordinate or abscissa of point P. Here $\overline{ON}$ = 2 units.

Length of $\overline{OM}$ is called the y-co-ordinate or ordinate of P. Here $\overline{OM}$ = 4 units.

Thus, the co-ordinates of point P are (2, 4) which is called an ordered pair.

So, the positions of the coordinates of a point in a plane cannot be interchanged as (4, 2).

Remember, if the distance of P from y-axis is ‘a’ and units the distance of P from the x-axis is ‘b’ units then the co-ordinates of point P are (a, b) where a denotes the x-co-ordinate or abscissa and b denotes the y-co-ordinate or ordinate.

Thus, we can define abscissa as distance of P from y-axis and ordinate as the distance of P from x-axis.

Point on x-axis: If we take any point on x-axis, then the distance of this point from x-axis is zero i.e., y-co-ordinate of every point on x-axis is zero.

Therefore, the co-ordinates of a point on x-axis are of the form (x, 0)

Point on y-axis: If we take any point on y-axis, then the distance of this point from y-axis is zero i.e., x-co-ordinate of every point on y-axis is zero.

Therefore, the co-ordinates of a point on y-axis are of the form (0, y).

Related Concepts:

● Coordinate Graph

● Ordered pair of a Coordinate System

● Plot Ordered Pairs

● Coordinates of a Point

● All Four Quadrants

● Signs of Coordinates

● Find the Coordinates of a Point

● Plot Points on Co-ordinate Graph

● Graph of Linear Equation

● Simultaneous Equations Graphically

● Graphs of Simple Function

● Graph of Perimeter vs. Length of the Side of a Square

● Graph of Area vs. Side of a Square

● Graph of Simple Interest vs. Number of Years

● Graph of Distance vs. Time

7th Grade Math Problems

8th Grade Math Practice

From Coordinates of a Point in a Plane to HOME PAGE