Conversion of Pure Recurring Decimal into Vulgar Fraction
Follow the steps for the conversion of pure recurring decimal into vulgar fraction:
(i) First write the decimal form by removing the bar from the top and put it equal to n (any variable).
(ii) Then write the repeating digits at least twice.
(iii) Now find the number of digits having bars on their heads.
● If the repeating decimal has 1 place repetition, then multiply both sides by 10.
● If the repeating decimal has 2 place repetitions, then multiply both sides by 100.
● If the repeating decimal has 3 place repetitions, then multiply both sides by 1000 and so on.
(iv) Then subtract the number obtained
in step (i) from the number obtained in step (ii).
(v) Then divide both the sides of the equation by the coefficient of n.
(vi) Therefore, we get the required vulgar fraction in the lowest form.
Worked-out examples for the conversion of pure recurring decimal into vulgar fraction:
1. Express 0.4 as a vulgar fraction.Solution:
Let n = 0.4
n = 0.444 ----------- (i)
Since, one digit is repeated after the decimal point, so we multiply both sides by 10.
Therefore, 10n = 4.44 ----------- (ii)
Subtracting (i) from (ii) we get;
10n - n = 4.44 - 0.44
9n = 4
n = 4/9 [dividing both the sides of the equation by 9]
Therefore, the vulgar fraction = 4/9
Solution:
Let n = 0.38
n = 0.3838 ----------------- (i)
Since, two digits are repeated after the decimal point, so we multiply both sides by 100.
Therefore, 100n = 38.38 ----------------- (ii)
Subtracting (i) from (ii) we get;
100n - n = 38.38 - 0.38
99n = 38
n = 38/99
Therefore, the vulgar fraction = 38/99
3. Express 0.532 as a vulgar fraction.
Solution:
Let n = 0.532
n = 0.532532 ----------------- (i)
Since, three digits are repeated after the decimal point, so we multiply both sides by 1000.
Therefore, 1000n = 532.532 ----------------- (ii)
Subtracting (i) from (ii) we get;
1000n - n = 532.532 - 0.532
999n = 532
n = 532/999
Therefore, the vulgar fraction = 532/999
Shortcut method for solving the problems on conversion of pure recurring decimal into vulgar fraction:
Write the recurring digits only once in the numerator and write as many nines in the denominator as is the number of digits repeated.
For example;
(a) 0.5Here numerator is the period (5) and the denominator is 9 because there is one digit in the period.
= 5/9
(b) 0.45Numerator = period = 45
Denominator = as many nines as the number of digits in the denominator
= 45/99
● Related Concept
● Decimals
● Conversion of Unlike Decimals to Like Decimals
● Decimal and Fractional Expansion
● Converting Decimals to Fractions
● Converting Fractions to Decimals
● H.C.F. and L.C.M. of Decimals
● Repeating or Recurring Decimal
● BODMAS/PEMDAS Rules - Involving Decimals
● PEMDAS Rules - Involving Integers
● PEMDAS Rules - Involving Decimals
● BODMAS Rules - Involving Integers
● Conversion of Pure Recurring Decimal into Vulgar Fraction
● Conversion of Mixed Recurring Decimals into Vulgar Fractions
● Rounding Decimals to the Nearest Whole Number
● Rounding Decimals to the Nearest Tenths
● Rounding Decimals to the Nearest Hundredths
● Simplify Decimals Involving Addition and Subtraction Decimals
● Multiplying Decimal by a Decimal Number
● Multiplying Decimal by a Whole Number
● Dividing Decimal by a Whole Number
● Dividing Decimal by a Decimal Number
From Conversion of Pure Recurring Decimal into Vulgar Fraction to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
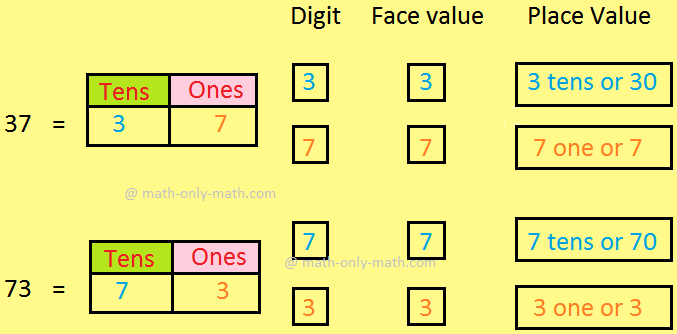
Math Place Value | Place Value | Place Value Chart | Ones and Tens
Apr 16, 25 03:10 PM
0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 are one-digit numbers. Numbers from 10 to 99 are two-digit numbers. Let us look at the digit 6 in the number 64. It is in the tens place of the number. 6 tens = 60 So… -
Place Value and Face Value | Place and Face Value of Larger Number
Apr 16, 25 02:55 PM
The place value of a digit in a number is the value it holds to be at the place in the number. We know about the place value and face value of a digit and we will learn about it in details. We know th… -
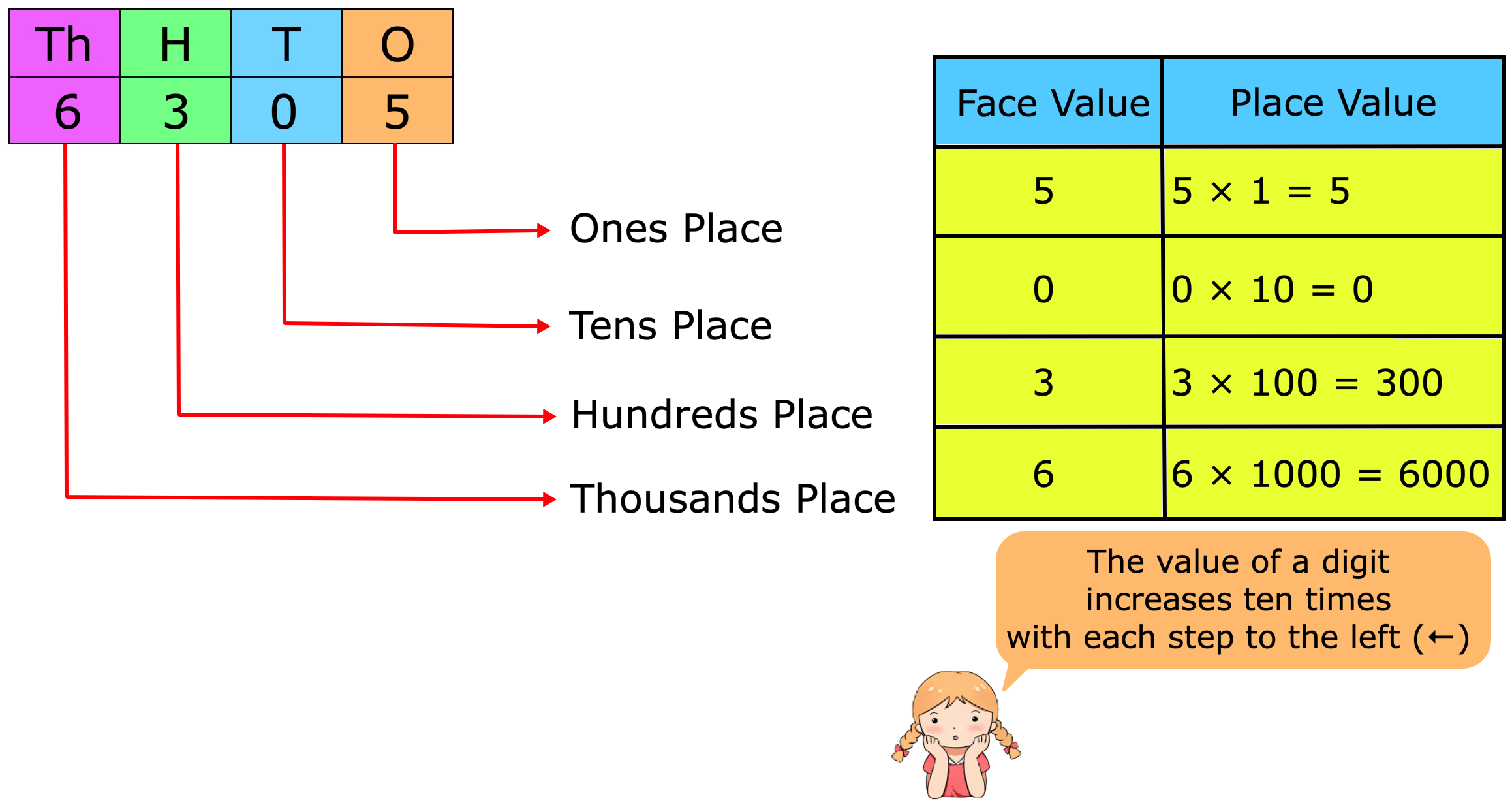
Face Value and Place Value|Difference Between Place Value & Face Value
Apr 16, 25 02:50 PM
What is the difference between face value and place value of digits? Before we proceed to face value and place value let us recall the expanded form of a number. The face value of a digit is the digit… -
Place Value and Face Value | Basic Concept on Place Value | Face Value
Apr 16, 25 02:44 PM
Learn the easiest way to understand the basic concept on place value and face value in the second grade. Suppose we write a number in figures 435 in words we write four hundred thirty five. -
Greater or Less than and Equal to | Bigger Number | Smaller Number | >
Apr 16, 25 02:31 PM
In math, greater or less than and equal to help the kids to understand how one number is different from the other number. Whether one number is bigger or smaller than the other number or both the numb



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.