Subscribe to our YouTube channel for the latest videos, updates, and tips.
Converse of Pythagorean Theorem
Converse of Pythagorean Theorem states that:
In a triangle, if the square of one side is equal to the sum of the squares of the other two sides then the angle opposite to the first side is a right angle.
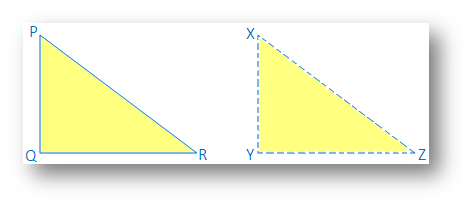
Given: A ∆PQR in which PR2 = PQ2 + QR2
To prove: ∠Q = 90°
Construction: Draw a ∆XYZ such that XY = PQ, YZ = QR and ∠Y = 90°
So, by Pythagora’s theorem we get,
XZ2 = XY2 + YZ2
⇒ XZ2 = PQ2 + QR2 ……….. (i), [since XY = PQ and YZ = QR]
But, PR2 = PQ2 + QR2 ………… (ii), [given]
From (i) and (ii) we get,
PR2 = XZ2 ⇒ PR = XZ
Now, in ∆PQR and ∆XYZ, we get
PQ = XY,
QR = YZ and
PR = XZ
Therefore ∆PQR ≅ ∆XYZ
Hence ∠Q = ∠Y = 90°
Word problems using the Converse of Pythagorean Theorem:
1. The side of a triangle are of length 4.5 cm, 7.5 cm and 6 cm. Is this triangle a right triangle? If so, which side is the hypotenuse?
Solution:
We know that hypotenuse is the longest side. If 4.5 cm, 7.5 cm and 6 cm are the lengths of angled triangle, then 7.5 cm will be the hypotenuse.
Using the converse of Pythagoras theorem, we get
(7.5)2 = (6)2 + (4.5)2⇒ 56.25 = 36 + 20.25
⇒ 56.25 = 56.25
Since, both the sides are equal therefore, 4.5 cm, 7.5 cm and 6 cm are the side of the right angled triangle having hypotenuse 7.5 cm.
2. The side of a triangle are of length 8 cm, 15 cm and 17 cm. Is this triangle a right triangle? If so, which side is the hypotenuse?
Solution:
We know that hypotenuse is the longest side. If 8 cm, 15 cm and 17 cm are the lengths of angled triangle, then 17 cm will be the hypotenuse.
Using the converse of Pythagoras theorem, we get
(17)2 = (15)2 + (8)2⇒ 289 = 225 + 64
⇒ 289 = 289
Since, both the sides are equal therefore, 8 cm, 15 cm and 17 cm are the side of the right angled triangle having hypotenuse 17 cm.
3. The side of a triangle are of length 9 cm, 11 cm and 6 cm. Is this triangle a right triangle? If so, which side is the hypotenuse?
Solution:
We know that hypotenuse is the longest side. If 9 cm, 11 cm and 6 cm are the lengths of angled triangle, then 11 cm will be the hypotenuse.
Using the converse of Pythagoras theorem, we get
(11)2 = (9)2 + (6)2⇒ 121 = 81 + 36
⇒ 121 ≠ 117
Since, both the sides are not equal therefore 9 cm, 11 cm and 6 cm are not the side of the right angled triangle.
The above examples of the converse of Pythagorean Theorem will help us to determine the right triangle when the sides of the triangles will be given in the questions.
Conditions for the Congruence of Triangles
Right Angle Hypotenuse Side congruence
Converse of Pythagorean Theorem
7th Grade Math Problems
8th Grade Math Practice
From Converse of Pythagorean Theorem to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Worksheet on Average | Word Problem on Average | Questions on Average
May 17, 25 05:37 PM
In worksheet on average interest we will solve 10 different types of question. Find the average of first 10 prime numbers. The average height of a family of five is 150 cm. If the heights of 4 family -
How to Find the Average in Math? | What Does Average Mean? |Definition
May 17, 25 04:04 PM
Average means a number which is between the largest and the smallest number. Average can be calculated only for similar quantities and not for dissimilar quantities. -
Problems Based on Average | Word Problems |Calculating Arithmetic Mean
May 17, 25 03:47 PM
Here we will learn to solve the three important types of word problems based on average. The questions are mainly based on average or mean, weighted average and average speed. -
Rounding Decimals | How to Round a Decimal? | Rounding off Decimal
May 16, 25 11:13 AM
Rounding decimals are frequently used in our daily life mainly for calculating the cost of the items. In mathematics rounding off decimal is a technique used to estimate or to find the approximate -
Worksheet on Rounding Off Number | Rounding off Number | Nearest 10
May 15, 25 05:12 PM
In worksheet on rounding off number we will solve 10 different types of problems. 1. Round off to nearest 10 each of the following numbers: (a) 14 (b) 57 (c) 61 (d) 819 (e) 7729 2. Round off to
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.