Binary Number System

Here we will discuss about the binary number system we already know binary numbers play a vital role in the design of digital computers.

Hence a detailed discussion of binary number system is given in this section. Binary number system uses two symbols 0 and 1 and its radix is 2. The symbols 0 and 1 are generally called BITS which is a contraction of the two words Binary digits.

An n-bit binary number of the form a_n-1 a_n-2 ….. a₁ a₀ where each a_i (i = 0, 1, …. n - 1) is either 0 or 1 has the magnitude.

a_n-1 2^n-1 + a_n-2 2^n-2 + …….+ a₁ 2¹ + a₀2⁰.

For fractional binary numbers, the base has negative integral powers starting with -1 for the bit position just after the binary point.

The bit at the extreme left of a binary number has the highest positional value and is usually called the Most Significant Bit or MSB. Similarly, the bit occupying the extreme right position of a given binary number has the least positional value and is referred to as the Least Significant Bit or LSB.

To facilitate the distinction between different number systems, we generally use the respective radix as a subscript of the number. However the subscript will not be used when there is no scope of confusion.

In binary number system a few examples on binary numbers and their decimal equivalents are given below:

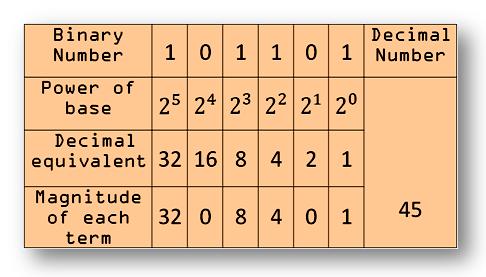
101101₂ = 1 × 2⁵ + 0 × 2⁴ + 1 × 2³ + 1 × 2² + 0 × 2¹ + 1 × 2⁰

= 32 + 0 + 8 + 4 + 0 + 1

= 45₁₀

The above results can be more clearly expressed in the following manner:

Binary point

111.1011₂

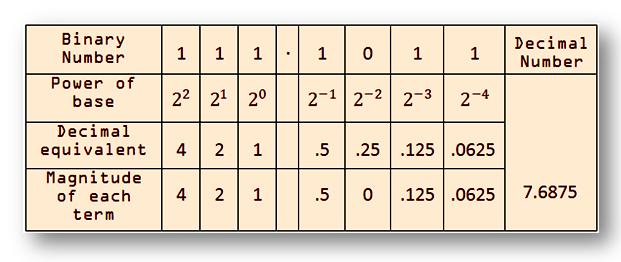
= 1 × 2² + 1 × 2¹ + 1 × 2⁰ + 1 × 2^-1 + 0 × 2^-2 + 1 × 2^-3 + 1 × 2^-4

= 4 + 2 + 1 + .5 + 0 + .125 + .0625

= 7.6875₁₀

The above results can be more clearly expressed in the following manner:

These are the basic examples shown above.

● Binary Numbers

• Data and Information

• Number System

• Decimal Number System

• Binary Number System

• Why Binary Numbers are Used

• Binary to Decimal Conversion

• Conversion of Numbers

• Octal Number System

• Hexa-decimal Number System

• Conversion of Binary Numbers to Octal or Hexa-decimal Numbers

• Octal and Hexa-Decimal Numbers

• Signed-magnitude Representation

• Radix Complement

• Diminished Radix Complement

• Arithmetic Operations of Binary Numbers

• Binary Addition

• Binary Subtraction

• Subtraction by 2’s Complement

• Subtraction by 1’s Complement

• Addition and Subtraction of Binary Numbers

• Binary Addition using 1’s Complement

• Binary Addition using 2’s Complement

• Binary Multiplication

• Binary Division

• Addition and Subtraction of Octal Numbers

• Multiplication of Octal Numbers

• Hexadecimal Addition and Subtraction

From Binary Number System to Home Page