Area of Combined Figures

A combined figure is a geometrical shape that is the combination of many simple geometrical shapes. 

To find the area of combined figures we will follow the steps:

Step I: First we divide the combined figure into its simple geometrical shapes. 

Step II: Then calculate the area of these simple geometrical shapes separately, 

Step III: Finally, to find the required area of the combined figure we need to add or subtract these areas.

Solved Examples on Area of combined figures:

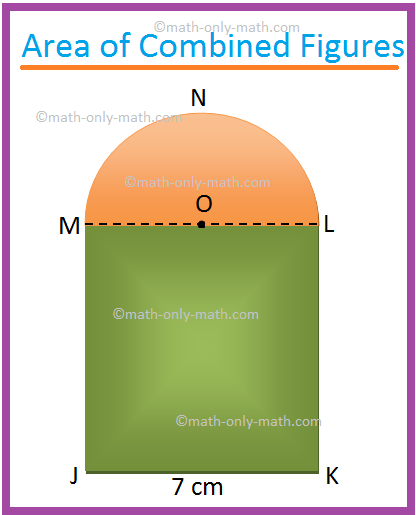
1. Find the area of the shaded region of the adjoining figure. (Use π = \(\frac{22}{7}\))

JKLM is a square of side 7 cm. O is the centre of the semicircle MNL.

Solution:

Step I: First we divide the combined figure into its simple geometrical shapes.

The given combined shape is combination of a square and a semicircle.

Step II: Then calculate the area of these simple geometrical shapes separately.

Area of the square JKLM = 7² cm²

                                    = 49 cm²

Area of the semicircle LNM = \(\frac{1}{2}\) π ∙ \((\frac{7}{2})^{2}\) cm² , [Since, diameter LM = 7 cm]

                                       = \(\frac{1}{2}\)  ∙  \(\frac{22}{7}\) ∙ \(\frac{49}{4}\) cm²

                                       = \(\frac{77}{4}\) cm²

                                       = 19.25 cm²

Step III: Finally, add these areas up to get the total area of the combined figure.

Therefore, the required area = 49 cm² + 19.25 cm²

                                          = 68.25 cm².

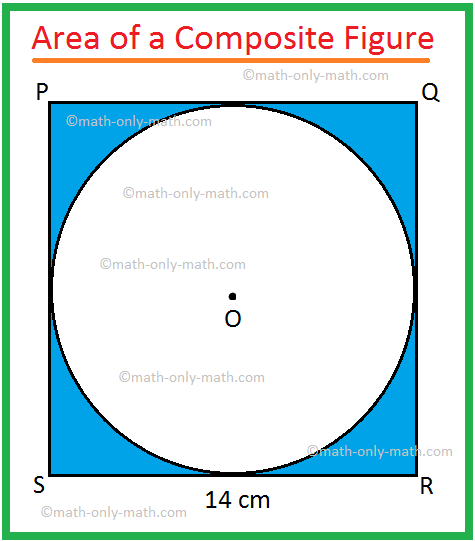
2. In the adjoining figure, PQRS is a square of side 14 cm and O is the centre of the circle touching all sides of the square. 

Find the area of the shaded region.

Solution:

Step I: First we divide the combined figure into its simple geometrical shapes.

The given combined shape is combination of a square and a circle.

Step II: Then calculate the area of these simple geometrical shapes separately.

Area of the square PQRS = 14² cm²

                                    = 196 cm²

Area of the circle with centre O = π ∙ 7² cm², [Since, diameter SR = 14 cm]

                                             = \(\frac{22}{7}\) ∙ 49 cm²

                                             = 22 × 7 cm²

                                             = 154 cm²

Step III: Finally, to find the required area of the combined figure we need to subtract the area of the circle from the area of the square.

Therefore, the required area = 196 cm² - 154 cm²

                                          = 42 cm²

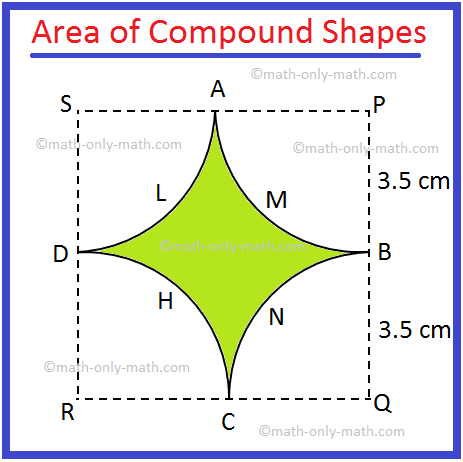
3. In the adjoining figure alongside, there are four equal quadrants of circles each of radius 3.5 cm, their centres being P, Q, R and S. 

Find the area of the shaded region.

Solution:

Step I: First we divide the combined figure into its simple geometrical shapes.

The given combined shape is combination of a square and four quadrants.

Step II:Then calculate the area of these simple geometrical shapes separately.

Area of the square PQRS = 7² cm², [Since, side of the square = 7 cm]

                                                = 49 cm²

Area of the quadrant APB = \(\frac{1}{4}\) π ∙ r² cm²

                                = \(\frac{1}{4}\) ∙ \(\frac{22}{7}\)  ∙  \((\frac{7}{2})^{2}\) cm², [Since, side of the square = 7 cm and radius of the quadrant = \(\frac{7}{2}\) cm]

                                = \(\frac{77}{8}\) cm²

There are four quadrants and they have the same area.

So, total area of the four quadrants = 4 × \(\frac{77}{8}\) cm²

                                                    = \(\frac{77}{2}\) cm²

                                                    = \(\frac{77}{2}\) cm²

Step III: Finally, to find the required area of the combined figure we need to subtract the area of the four quadrants from the area of the square.

Therefore, the required area = 49 cm² - \(\frac{77}{2}\) cm²

                                          = \(\frac{21}{2}\) cm²

                                          = 10.5 cm²

10th Grade Math

From Areas of Combined Figures to HOME PAGE