Area and Perimeter of Combined Figures
Here we will solve different types of problems on finding the area and perimeter of combined figures.
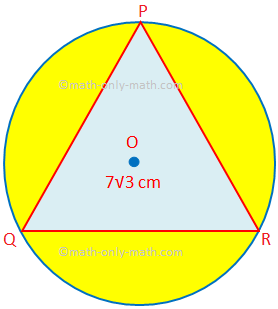
1. Find the area of the shaded region in which PQR is an equilateral triangle of side 7√3 cm. O is the centre of the circle.
(Use π = 227 and √3 = 1.732.)
Solution:
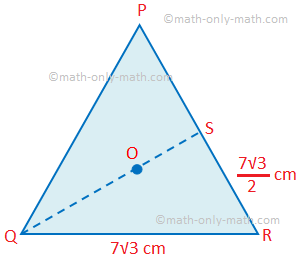
The centre O of the circle is the circumcentre of the equilateral triangle PQR.
So, O is also the centroid of the equilateral triangle and QS ⊥ PR, OQ = 2OS. If the radius of the circle be r cm then
OQ = r cm,
OS = r2 cm,
RS = 12 PR = 7√32 cm
Therefore, QS2 = QR2 - RS2
or, (3r2)2 = (7√3)2 - (7√32)2
or, 94 r2 = (1 - 14) (7√3)2
or, 94 r2 = 34 × 49 × 3
or, r2 = 34 × 49 × 3 × 49
or, r2 = 49
Therefore, r = 7
Therefore, area of the shaded region = Area of the circle – Area of the equilateral triangle
= πr2 - √34 a2
= 227 × 72 cm2 - √34 × (7√3)2 cm2
= (154 - √34 × 147) cm2
= (154 - 1.732×1474) cm2
= (154 - 254.6044) cm2
= (154 - 63.651) cm2
= 90349 cm2
2. The radius of the wheels of a car is 35 cm. The car takes 1 hour to cover 66 km. Find the number of revolutions that a wheel of the car makes in one minute. (Use π = 227.)
Solution:
According to the problem, radius of a wheel = 35 cm.
The perimeter of a wheel = 2πr
= 2 × 227 × 35 cm
= 220 cm
Therefore, the number of revolutions of a wheel to cover 66 km = 66km220km
= 66×1000×100cm220cm
= 3×1000×10010
= 30000
Therefore, the number of revolutions of a wheel to make in
one minute = 3000060
= 500
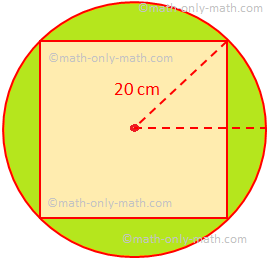
3. A circular piece of paper of radius 20 cm is trimmed into the shape of the biggest possible square. Find the area of the paper cut off. (Use π = 227.)
Solution:
The area of the piece of paper = πr2
= 227 × 202 cm2
If the side of the inscribed square be x cm then
202 = (x2)2 + (x2)2
or, 400 = 12 x2
or, x2 = 800.
Therefore, the area of the paper cut off = The area of the circle - The area of the square
= πr2 - x2
= 227 × 202 cm2 - 800 cm2
= (88007 - 800) cm2
= 32007 cm2
= 45717 cm2
From Area and Perimeter of Combined Figures to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Vertical Subtraction | Examples | Word Problems| Video |Column Method
Mar 22, 25 05:20 PM
Vertical subtraction of 1-digit number are done by arranging the numbers column wise i.e., one number under the other number. How to subtract 1-digit number vertically? -
Worksheet on 11 Times Table | Printable Multiplication Table | Video
Mar 22, 25 05:08 PM
Worksheet on 11 times table can be printed out. Homeschoolers can also use these multiplication table sheets to practice at home. -
Worksheet on 10 Times Table | Printable Multiplication Table | Video
Mar 21, 25 03:46 PM
Worksheet on 10 times table can be printed out. Homeschoolers can also use these multiplication table sheets to practice at home. -
5th Grade Prime and Composite Numbers | Definitions | Examples | Math
Mar 21, 25 12:18 AM
5th grade prime and composite numbers -
14 Times Table | Read and Write Multiplication Table of 14| Video
Mar 20, 25 04:03 PM
In 14 times table we will learn how to read and write multiplication table of 14. We read fourteen times table as:One time fourteen is 14 Two times fourteen are 28 Three times fourteen are 42




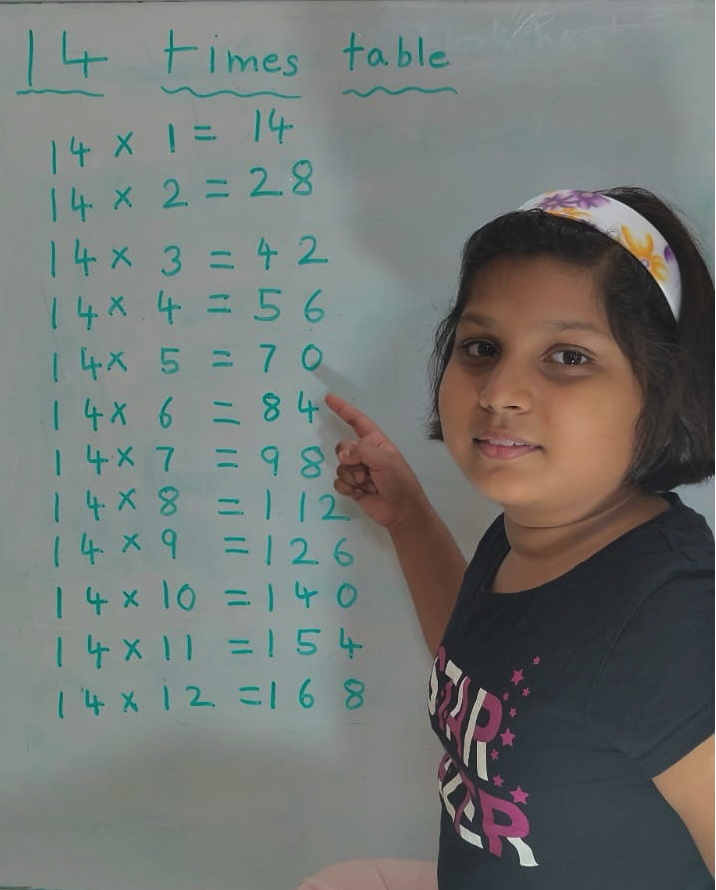
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.