Application of Basic Proportionality Theorem
Here we will prove that the internal bisector of an angle of a triangle divides the opposite side in the ratio of the sides containing the angle.
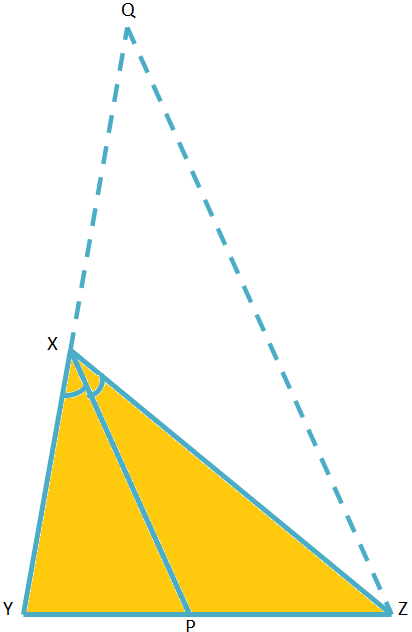
Given: XP is the internal bisector of ∠YXZ, intersecting YZ at P.
To prove: \(\frac{YP}{PZ}\) = \(\frac{XY}{XZ}\).
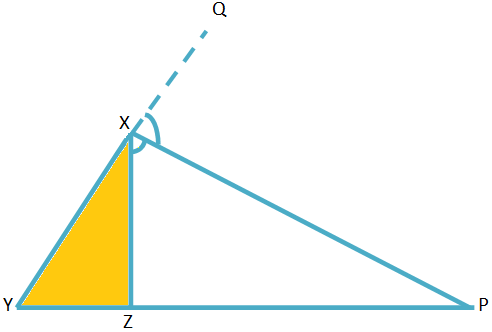
Construction: Draw ZQ ∥ XP such that ZQ meets YX produced at Q.
Proof:
|
Statement 1. ∠YXP = ∠XQZ 2. ∠PXZ = ∠XZQ 3. ∠XQZ = ∠XZQ 4. XQ = XZ 5. \(\frac{YX}{XQ}\) = \(\frac{YP}{PZ}\) 6. \(\frac{YX}{XZ}\) = \(\frac{YP}{PZ}\) |
Reason 1. XP ∥ QZ and YQ is a transversal 2. XP ∥ QZ and XZ is a transversal 3. ∠YXP = ∠PXZ 4. ∠XQZ = ∠XZQ 5. XP ∥ QZ 6. By statement 4. |
Note:
1. The above proposition is true for external division also.
So, \(\frac{YP}{ZP}\) = \(\frac{XY}{XZ}\)
2. Converse of the above proposition is also true.
So, if P is a point on YZ such that YP : PZ = XY : XZ then XP bisects the angle YXZ internally or externally.
From Application of Basic Proportionality Theorem to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.