Subscribe to our YouTube channel for the latest videos, updates, and tips.
Angle Side Angle Congruence
Conditions for the ASA - Angle Side Angle congruence
Two triangles are said to be congruent if two angles and the included side of the one are respectively equal to the two angles and the included side of the other.
Experiment to prove Congruence with ASA:
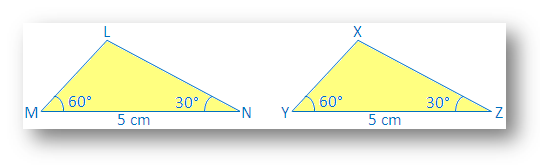
Draw a ∆LMN with ∠M = 60°, MN = 5 cm, ∠N = 30°.
Also, draw another ∆XYZ with ∠Y = 60°, YZ = 5cm, ∠Z = 30°.
We see that ∠M = ∠Y, MN = YZ and ∠N = ∠Z.
Make a trace copy of ∆XYZ and try to make it cover ∆LMN with X on L, Y on M and Z on N.
We observe that: two triangles cover each other exactly.
Therefore ∆LMN ≅ ∆XYZ
Worked-out problems on angle side angle congruence triangles (ASA postulate):
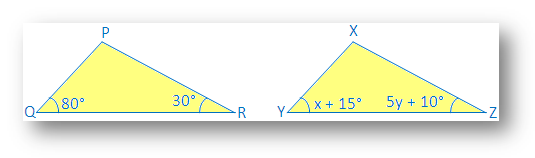
1. ∆PQR ≅ ∆XYZ by ASA congruence condition. Find the value of x and y.
Solution:
WE know ∆ PQR ≅ ∆XYZ by ASA congruence.
Therefore ∠Q = ∠Y i.e., x + 15 = 80° and ∠R = ∠Z i.e., 5y + 10 = 30°.
Also, QR = YZ.
Since, x + 15 = 80°
Therefore x = 80 – 15 = 65°
Also, 5y + 10 = 30°
So, 5y = 30 – 10
Therefore, 5y = 20
⇒ y = 20/5
⇒ y = 4°
Therefore, the value of x and y are 65° and 4°.
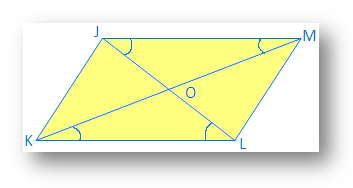
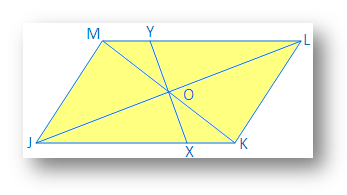
2. Prove that the diagonals of a parallelogram bisect each other.
In a parallelogram JKLM, diagonal JL and KM intersect at O
It is required to prove that JO = OL and KO = OM
Proof: In ∆JOM and ∆KOL
∠OJM = ∠OLK [since, JM ∥ KL and JL is the transversal]
JM = KL [opposite sides of a parallelogram]
∠OMJ = ∠OKL [since, JM ∥ KL and KM is the transversal]
Therefore, ∆JOM and ∆KOL [Angle-Side-Angel]
Therefore, JO = OL and KO = OM [Sides of congruent triangle]
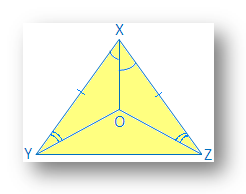
3. ∆XYZ is an equilateral triangle such that XO bisects ∠X.
Also, ∠XYO = ∠XZO. Show that ∆YXO ≅ ∆ZXO
Solution:
∆ XYZ is an equilateral
Therefore, XY = YZ = ZX
Given: XY bisects ∠X.
Therefore, ∠YXO = ∠ZXO
Given: ∠XYO = ∠XZO
Given: XY = XZ
Therefore, ∆YXO ≅ ∆ZXO by ASA congruence condition
4. The straight line drawn through the intersection of the two diagonals of a parallelogram divide it into two equal parts.
Solution:
O is the point of intersection of the two diagonals JL and KM of the parallelogram JKLM.
Straight line XOY meets JK and LM at the point X and Y respectively.
It is required to prove that quadrilateral JXYM equal to quadrilateral LYXK.
Proof: In ∆JXO and ∆LYO, JO = OL [diagonals of a parallelogram bisect each other]
∠OJX= alternate ∠OLY
∠JOX = ∠LOY
Therefore, ∆ JOX ≅ ∆ LOY [by angle side angle congruence]
Therefore, JX = LY
Therefore, KX = MY [since, JK = ML]
Now in quadrilaterals JXYM and LYXK, JX = LY; XY = YX, YM = XK and MJ = KL and ∠MJX = ∠KLY
Hence it is proved that in the two quadrilaterals the sides are equal to each other and the included angles of two equal sides are also equal.
Therefore, quadrilateral JXYM equal to quadrilateral XKLY.
Conditions for the Congruence of Triangles
Right Angle Hypotenuse Side congruence
Converse of Pythagorean Theorem
7th Grade Math Problems
8th Grade Math Practice
From Angle Side Angle Congruence to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Expanded form of Decimal Fractions |How to Write a Decimal in Expanded
May 07, 25 01:48 AM
Decimal numbers can be expressed in expanded form using the place-value chart. In expanded form of decimal fractions we will learn how to read and write the decimal numbers. Note: When a decimal is mi… -
Dividing Decimals Word Problems Worksheet | Answers |Decimals Division
May 07, 25 01:33 AM
In dividing decimals word problems worksheet we will get different types of problems on decimals division word problems, dividing a decimal by a whole number, dividing a decimals and dividing a decima… -
How to Divide Decimals? | Dividing Decimals by Decimals | Examples
May 06, 25 01:23 AM
Dividing Decimals by Decimals I. Dividing a Decimal by a Whole Number: II. Dividing a Decimal by another Decimal: If the dividend and divisor are both decimal numbers, we multiply both the numbers by… -
Multiplying Decimal by a Whole Number | Step-by-step Explanation|Video
May 06, 25 12:01 AM
Multiplying decimal by a whole number is just same like multiply as usual. How to multiply a decimal by a whole number? To multiply a decimal by a whole number follow the below steps -
Word Problems on Decimals | Decimal Word Problems | Decimal Home Work
May 05, 25 01:27 AM
Word problems on decimals are solved here step by step. The product of two numbers is 42.63. If one number is 2.1, find the other. Solution: Product of two numbers = 42.63 One number = 2.1
New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.