Amplitude or Argument of a Complex Number
To find the Amplitude or Argument of a complex number let us assume that, a complex number z = x + iy where x > 0 and y > 0 are real, i = √-1 and x2 + y2 ≠ 0; for which the equations x = |z| cos θ and y = |z| sin θ are simultaneously satisfied then, the value of θ is called the Argument (Agr) of z or Amplitude (Amp) of z.
From the above equations x = |z| cos θ and y = |z| sin θ satisfies infinite values of θ and for any infinite values of θ is the value of Arg z. Thus, for any unique value of θ that lies in the interval - π < θ ≤ π and satisfies the above equations x = |z| cos θ and y = |z| sin θ is known as the principal value of Arg z or Amp z and it is denoted as arg z or amp z.
We know that, cos (2nπ + θ) = cos θ and sin (2nπ + θ) = sin θ (where n = 0, ±1, ±2, ±3, .............), then we get,
Amp z = 2nπ + amp z where - π < amp z ≤ π
Algorithm for finding
Argument of z = x + iy
Step I: Find the value of tan−1 |yx| lying between 0 and π2. Let it be α.
Step II: Determine in which quadrant the point M(x, y) belongs.
If M (x, y) belongs to the first quadrant, then arg (z) = α.
If M (x, y) belongs to the second quadrant, then arg (z) = π - α.
If M (x, y) belongs to the third quadrant, then arg (z) = - (π - α) or π + α
If M (x, y) belongs to the fourth quadrant, then arg (z) = -α or 2π - α
Solved Examples to find the Argument or Amplitude of a complex number:
1. Find the argument of the complex number i1−i.
Solution:
The given complex number i1−i
Now multiply the numerator and denominator by the conjugate of the denominator i.e., (1 + i), we get
i(1+i)(1−i)(1+i)
= i+i2)(1−i2
= i−12
= - 12 + i ∙ 12
We see that in the z-plane the point z = - 12 + i ∙ 12 = (-12, 12) lies in the second quadrant. Hence, if amp z = θ then,
tan θ = 12−12 = -1, where π2 < θ ≤ π
Thus, tan θ = -1 = tan (π- π4) = tan 3π4
Therefore, required argument of i1−i is 3π4.
2. Find the argument of the complex number 2 + 2√3i.
Solution:
The given complex number 2 + 2√3i
We see that in the z-plane the point z = 2 + 2√3i = (2, 2√3) lies in the first quadrant. Hence, if amp z = θ then,
tan θ = 2√32 = √3, where θ lying between 0 and π2.
Thus, tan θ = √3 = tan π3
Therefore, required argument of 2 + 2√3i is π3.
11 and 12 Grade Math
From Amplitude or Argument of a Complex Number to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
Recent Articles
-
Divisible by 10 | Test of Divisibility by 10 Video | Rules | Examples
Mar 29, 25 03:06 PM
Divisible by 10 is discussed below. A number is divisible by 10 if it has zero (0) in its units place. Consider the following numbers which are divisible by 10, using the test of divisibility by 10: -
Divisible by 9 | Test of Divisibility by 9 | Rules | Video | Examples
Mar 29, 25 02:55 PM
A number is divisible by 9, if the sum is a multiple of 9 or if the sum of its digits is divisible by 9. Consider the following numbers which are divisible by 9, using the test of divisibility by 9: -
Divisible by 6 | Rules for Test of Divisibility by 6 Video | Examples
Mar 29, 25 02:48 PM
Divisible by 6 is discussed below: A number is divisible by 6 if it is divisible by 2 and 3 both. Consider the following numbers which are divisible by 6, using the test of divisibility by 6: 42 -
Divisible by 5 | Rules for Test of divisibility by 5 | Video |Examples
Mar 29, 25 02:43 PM
Divisible by 5 is discussed below: A number is divisible by 5 if its units place is 0 or 5. Consider the following numbers which are divisible by 5, using the test of divisibility by -
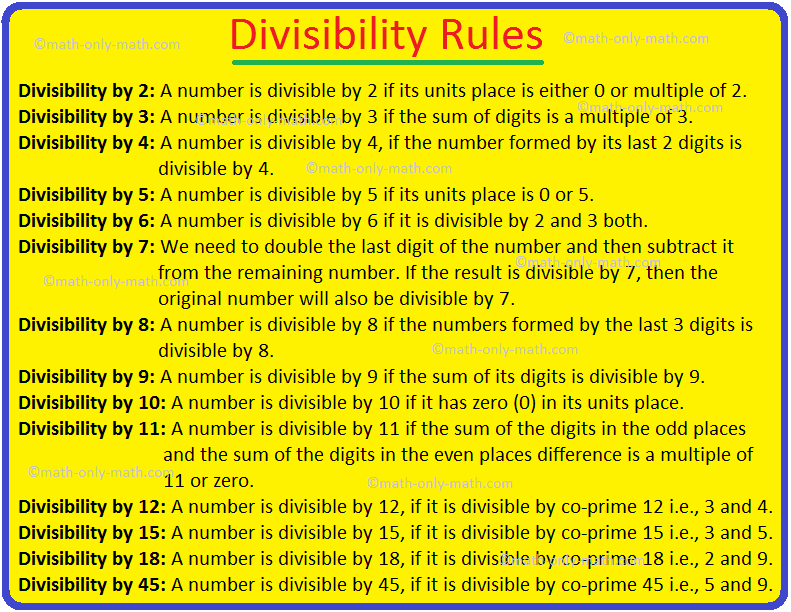
Divisibility Rules From 2 to 18 | Math Divisibility Test | Videos |
Mar 29, 25 02:17 PM
To find out factors of larger numbers quickly, we perform divisibility test. There are certain rules to check divisibility of numbers. Divisibility tests of a given number by any of the number 2, 3, 4…





New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.