Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.
6th Grade Algebra
Algebra is one of the branches of mathematics that involves letters of the English alphabet, numbers, and mathematical operations.
In simplest way Algebra is a generalized form of Arithmetic.
In Arithmetic we only deal with numbers. There we include different operations on numbers which have one single definite value.
But in the algebra we not only deal with numbers, we deal with some letters also which represent different numbers. These letters may have any value we choose to assign to them. There is no restriction to the numerical values a letter may represent.
Suppose for example, let 'x = 1', that does not mean that x must always have the value 1, but only for this example we can consider x = 1.
For Example:
5x, 2x + 5, 2a + 2, y - 2x, x + 10y, x + 2y - 3z, etc.
Suppose, we consider three circles of radii 7 cm, 8 cm and 9 cm.
We can say here that are three circles of radius r cm, where, ‘r’ represents different numbers.
The letters used in Algebra are called Variables or literal number or simply literals.
Generally in algebra we operate letters or symbols without assigning any particular numerical value at all.
According to the definition of algebra, premising that the signs +, -, × and ÷ are used with the same meaning as in Arithmetic.
Also, the following sign and symbols are frequently used in algebra and have the same meanings as they have in any other branch of Mathematics.
= means, "is equal to"
≠ means, "is not equal to"
< means, "is less than"
> means, "is greater than"
≮ means, "is not less than"
≯ means, "is not greater than"
∴ means, "therefore"
∵ means, "because" or "since"
~ means, "difference between"
⇒ means, "implies that"
Main Features of Algebra:
The main feature of algebra is the use of letters, which allow us to write rules and formulae in the general way and one can talk about any number and not just a particular number.
● Letters may stand for unknown quantities. By learning methods of determining unknowns, we develop powerful tools for solving puzzles and problems from daily life.
● Since letters stand for numbers, operations can be performed on them as numbers. This leads to the study of algebraic expressions and their properties
Patterns:
(i) Number Patterns:
Number patterns can be used to help discovering ways to represent certain types of numbers using variables.
Working Rules for Solving Number Patterns:
Step I: Take any number.
Step II: Perform the number operations such as addition, subtraction, multiplication or
division with that number.
Step III: Try to obtain the relationship within the result of various number of operations.
Step IV: Find that when any number is again and again added, multiplied, subtracted. divided, squared or cubed, a pattern is formed. Instead of performing these operations again and again, a letter is used to denote these operations to avoid difficulty.
For Example:
Let us find out a pattern for even numbers:
|
1 × 2 = 2 3 × 2 = 6 5 × 2 = 10 8 × 2 = 16 15 × 2 = 30 |
(2 is an even number.) (6 is an even number.) (10 is an even number) (16 is an even number.) (30 is an even number.) |
From the above pattern, we can say that when an integer is multiplied by 2, it gives an even number.
In general, if n is any integer, then 2n represents an even number.
(ii) Dot Patterns:
Dot patterns can be used to help discovering ways to represent certain types of numbers using dots.
Working Rules for Solving Dot Patterns:
Same as the number patterns except that dots are used in place of numbers.
For Example:
1. Find a pattern for the first four square numbers through dots:
Solution:
Thus, a pattern for the first four square numbers is n2.
(iii) Patterns from Matchsticks:
Matchstick patterns can be used to help discovering ways to represent certain type of numbers in the form of shapes using matchsticks.
Working Rules for Solving Patterns from Matchsticks:
Step I: Write an expression in terms of n, for the number of matchsticks in the nth shape.
Step II: Find the general rule to find the nth term.
For Example:
1. Find out the pattern for the shape 'hexagon' through matchsticks.
Solutions:
Observe the following:
1st shape contains 6 (= 1 × 5 + 1 ) matchsticks.
2nd shape contains 11 (= 2 × 5 + 1 ) matchsticks.
3rd shape contains 16 (= 3 × 5 + 1 ) matchsticks.
4th shape contains 21 (= 4 × 5 + 1 ) matchsticks.
Now, we can say that the ith shape will contain 5n + 1 matchsticks.
Also, 315th term of the sequence 6, 11, 16, 21, .... is
5 × 315 + 1 = 1576
(iv) Number Sequences or Finding Any Number in a Sequence:
Each number in a sequence is called a term.
Working Rules for Solving Number Sequences or Finding Any Number in a Sequence:
Step I: First, find the rule which helps to find the next or missing term.
Step II: Then, find the general rule to find the nth term.
For Example:
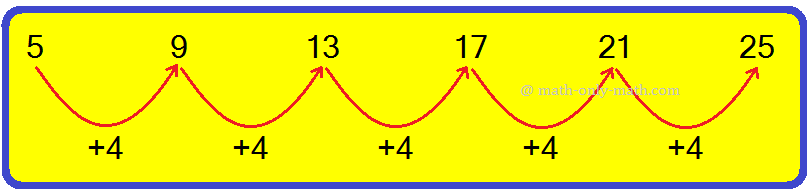
Consider the following sequence:
5, 9, 13, 17, 21, 25, ...........
In the above sequence, each succeeding term is obtained on adding 4 to the preceding term.
So, the rule 'to add 4'.
1st term 5 = 4 × 1 + 1
2nd term 9 = 4 × 2 + 1
3rd term 13 = 4 × 3 + 1
4th term 17 = 4 × 4 + 1
Therefore, the nth term = 4n + 1 .
Solved Example:
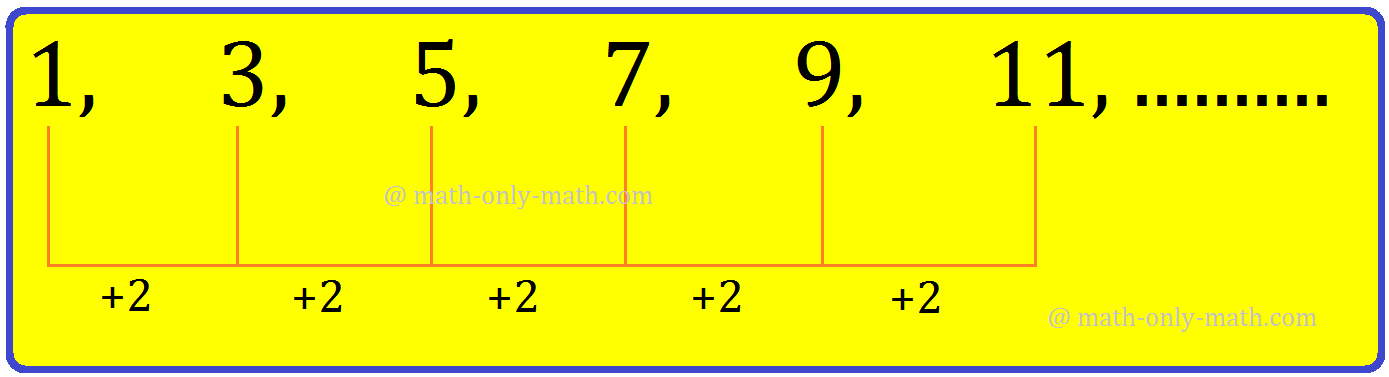
2. Write the next two terms in the series 1, 3, 5, 7, 9, 11,........
Solution:
In the given series,
The next two terms: 11 + 2 = 13, 13 + 2 = 15
Algebra
Properties of Multiplication of Literals
● Literal Numbers - Worksheets
Worksheet on Addition of Literals
Worksheet on Subtraction of Literals
Worksheet on Multiplication of Literals
Worksheet on Division of Literals
Worksheet on Powers of Literal Numbers
● Constants and Variables - Worksheet
Worksheet on Constants and Variables
● Terms
Adding and Subtracting Like Terms
● Terms - Worksheets
Worksheet on Like and Unlike Terms
● Terms of an Algebraic Expression
Types of Algebraic Expressions
Multiplication of Two Monomials
Multiplication of Polynomial by Monomial
Multiplication of two Binomials
Division of Polynomial by Monomial
Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.
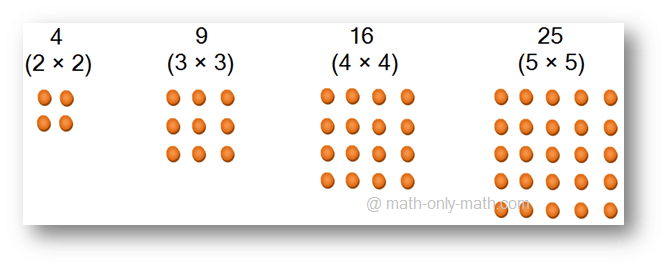



New! Comments
Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.