90 Degree Clockwise Rotation

Learn about the rules for 90 degree clockwise rotation about the origin.

How do you rotate a figure 90 degrees in clockwise direction on a graph?

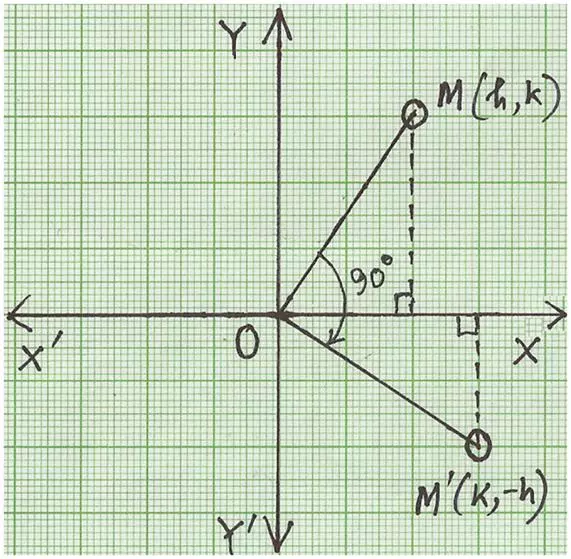
Rotation of point through 90° about the origin in clockwise direction when point M (h, k) is rotated about the origin O through 90° in clockwise direction. The new position of point M (h, k) will become M’ (k, -h).

Worked-out examples on 90 degree clockwise rotation about the origin:

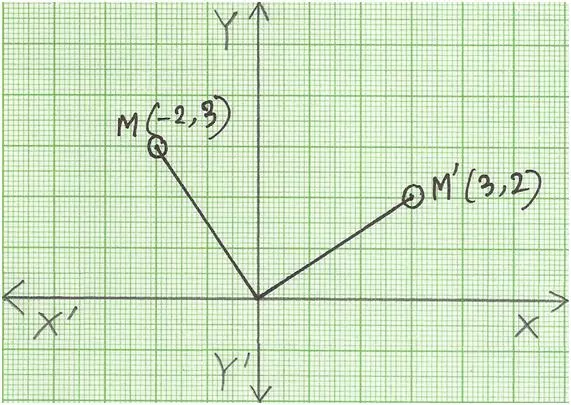
1. Plot the point M (-2, 3) on the graph paper and rotate it through 90° in clockwise direction, about the origin. Find the new position of M.

Solution:

When the point is rotated through 90° clockwise about the origin, the point M (h, k) takes the image M' (k, -h).

Therefore, the new position of point M (-2, 3) will become M' (3, 2).

2. Find the co-ordinates of the points obtained on rotating the point given below through 90° about the origin in clockwise direction.

(i) P (5, 7)            

(ii) Q (-4, -7)       

(iii) R (-7, 5)        

(iv) S (2, -5)

Solution:

When rotated through 90° about the origin in clockwise direction, the new position of the above points are;

(i) The new position of point P (5, 7) will become P' (7, -5)           

(ii) The new position of point Q (-4, -7) will become Q' (-7, 4)      

(iii) The new position of point R (-7, 5) will become R' (5, 7)

(iv) The new position of point S (2, -5) will become S' (-5, -2)

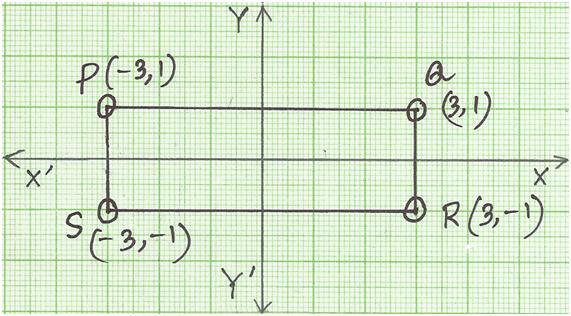
3. Construct the image of the given figure under the rotation of 90° clockwise about the origin O.

Solution:

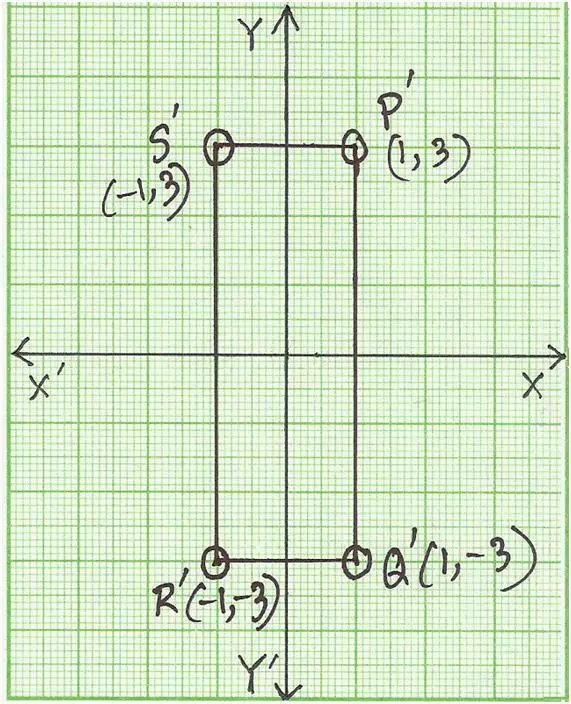
We get rectangular PQRS by plotting the points P (-3, 1), Q (3, 1), R (3, -1), S (-3, -1).  When rotated through 90°, P' (1, 3), Q' (1, -3), R' (-1, -3) and S' (-1, 3).

Now join P'Q'R'S'.

Therefore, P'Q'R'S' is the new position of PQRS when it is rotated through 90°.

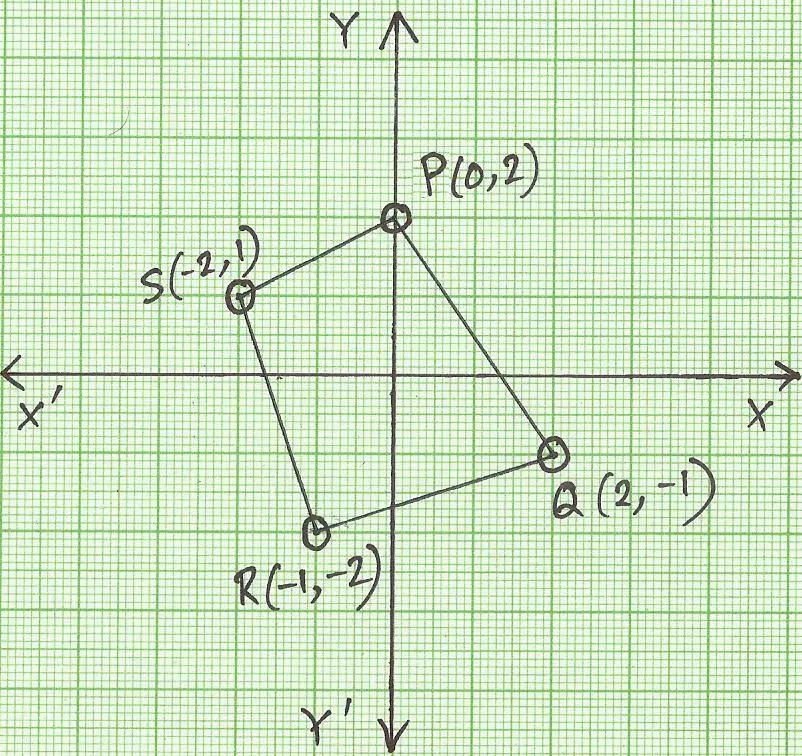
4. Draw a quadrilateral PQRS joining the points P (0, 2), Q (2, -1), R (-1, -2) and S (-2, 1) on the graph paper. Find the new position when the quadrilateral is rotated through 90° clockwise about the origin.

Solution:

Plot the point P (0, 2), Q (2, -1), R (-1, -2) and S (-2, 1) on the graph paper. Now join PQ, QR, RS and SP to get a quadrilateral. On rotating it through 90° about the origin in clockwise direction, the new positions of the points are

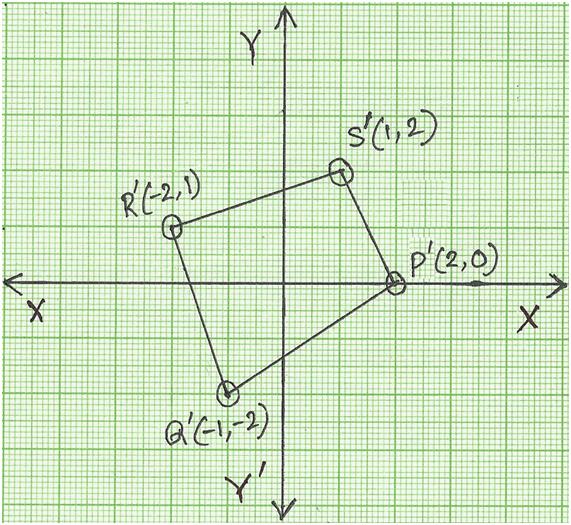
The new position of point P (0, 2) will become P' (2, 0)

The new position of point Q (2, -1) will become Q' (-1, -2)

The new position of point R (-1, -2) will become R' (-2, 1)

The new position of point S (-2, 1) will become S' (1, 2)

Thus, the new position of quadrilateral PQRS is P'Q'R'S'.

● Related Concepts

● Lines of Symmetry

● Point Symmetry

● Rotational Symmetry

● Order of Rotational Symmetry

● Types of Symmetry

● Reflection

● Reflection of a Point in x-axis

● Reflection of a Point in y-axis

● Reflection of a point in origin

● Rotation

● 90 Degree Clockwise Rotation

● 90 Degree Anticlockwise Rotation

● 180 Degree Rotation

7th Grade Math Problems

8th Grade Math Practice

From 90 Degree Clockwise Rotation to HOME PAGE