Construction of Perpendicular Lines

Construction of perpendicular lines by using a protractor is discussed here.

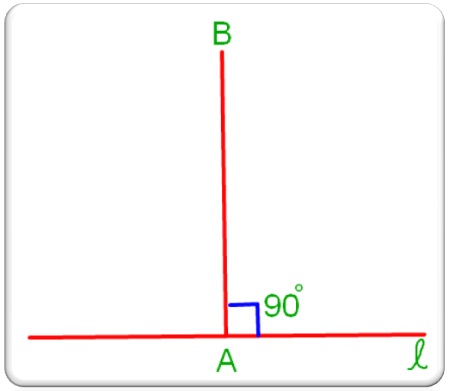
Perpendicular lines are lines that intersect at right angles (90°).

The symbol '⊥' means "is perpendicular to".

For example: The corners of a room walls are perpendicular to each other.

I: Construction of a Perpendicular Line to a Line Through a Point on it:

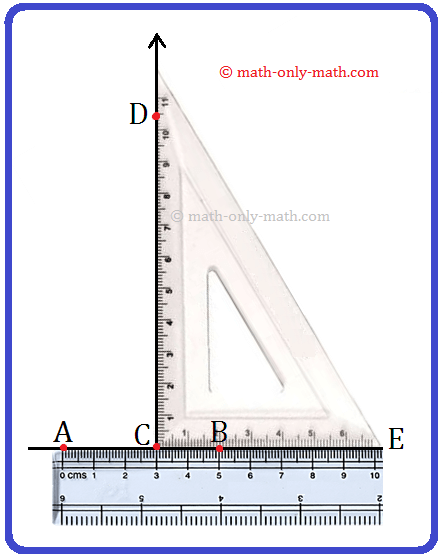
First Method: Using Scale/Ruler and Set-Square

You are given a line, say $\overline{AB}$. Can you draw a perpendicular line to $\overline{AB}$ on a point P (say) of it? Follow the Working Rules given below to draw such perpendicular line.

Working Rules for Construction of Perpendicular Lines using Scale and Set-Square:

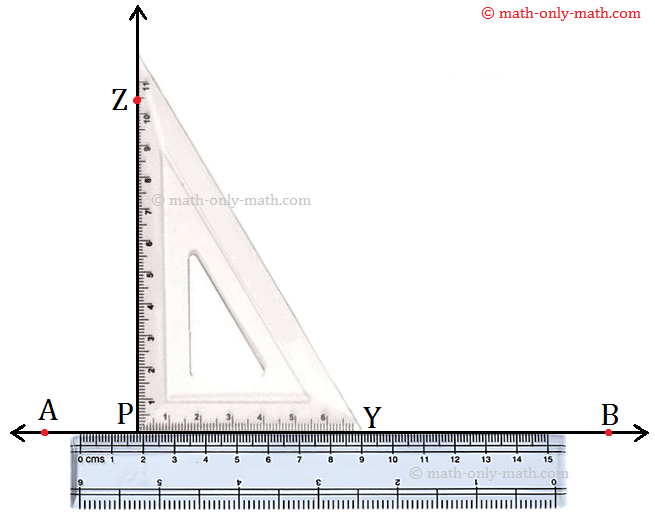
Step 1: Place a scale along the line AB as shown in the following figure.

Step 2: Place the set-square with its shortest side along AB above the scale.

Step 3: Slide the set-square firmly along $\overleftrightarrow{AB}$ until its point Z coincides with the given point P

Step 4: Holding the set-square firmly, trace the line $\overleftrightarrow{PZ}$ along the edge of the set-square. Thus, PZ is perpendicular to AB at P. We can write it as $\overleftrightarrow{PZ}$ ⊥ $\overleftrightarrow{AB}$

Second Method: Using Scale/Ruler and Set-Square

Follow the Working Rules given on the following to draw a perpendicular line to a line segment, say AB, using ruler and compass.

Working Rules for Construction of Perpendicular Lines using Scale and Compass:

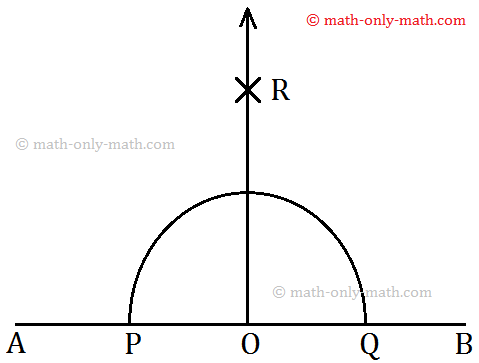
Step 1: Mark a point O on AB. With O as centre and a suitable radius, draw an arc to cut $\overline{AB}$ at P and Q.

Step 2: With P as centre and taking a radius of more than PO, draw an arc on one side of $\overline{AB}$.

Step 3: With Q as centre and taking the same radius, draw another arc to intersect the previous arc at R.

Step 4: The line through R and O is drawn. Now, $\overleftrightarrow{OR}$ is the required perpendicular to $\overline{AB}$ through O.

II: Construction of a Perpendicular Line Through a Point Not on it:

First Method: Using Scale/Ruler and Set-Squares:

Let us draw a perpendicular line to a line AB (say) from an outside point P.

Working Rules for Construction of Perpendicular Lines using Scale and Set-Square:

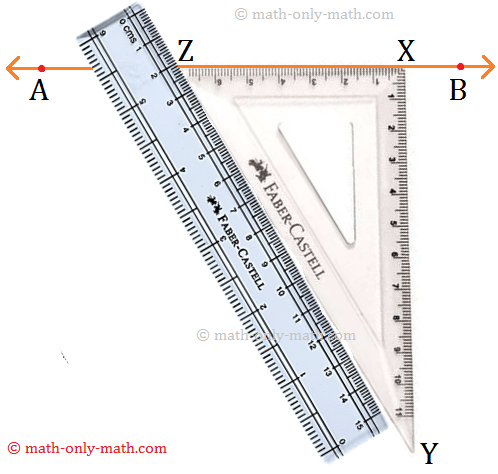
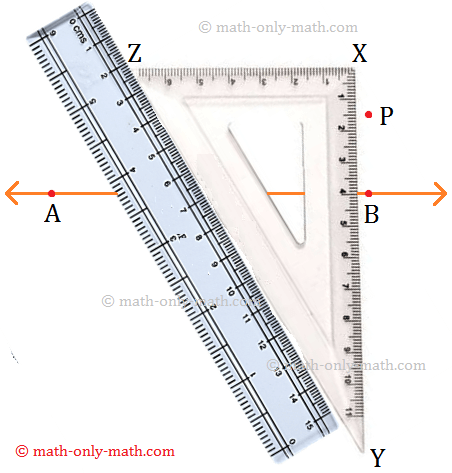
Step 1: Place a set-square XYZ just below the line AB in such a way that one of its sides containing right angle touches the line.

Step 2: Hold the set-square firmly and place a scale such that its edge is positioned along YZ of the set-squre.

Step 3: Holding the ruler firmly, slide the set- square along the scale until the side XY of the set square passes through the given point P.

Step 4: Keeping the set-square in this position, trace the line XY along the edge of the set- square. Thus, XY is the perpendicular line to the given line AB passing through the point P.

Second Method: Using Scale/Ruler and Compass:

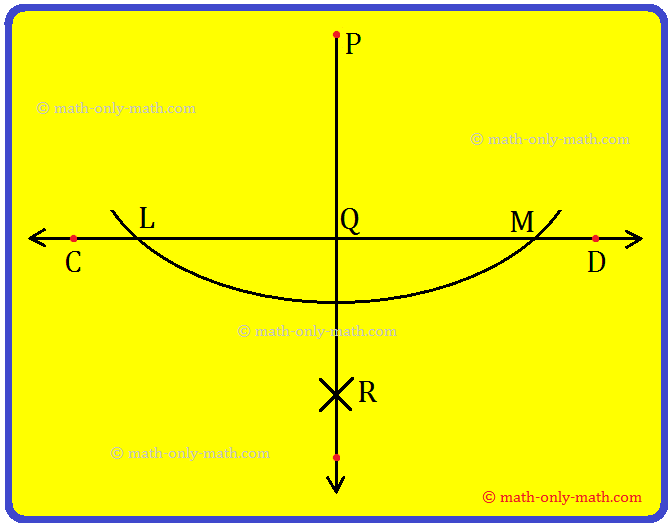
Let us draw a perpendicular line to a line AB (say) through a point O located outside the line.

Working Rules for Construction of Perpendicular Lines using Scale and Compass:

Step 1: Draw $\overline{AB}$ of any length and mark a point O outside it.

Step 2: With O as centre and a suitable radius, draw an arc to cut $\overline{AB}$ at Land M respectively.

Step 3: With L as and taking a radius greater than $\frac{1}{2}$$\overline{LM}$. draw an arc.

Step 4: With Mas centre and the same radius as in step 2, draw another arc to cut the previous arc at R.

Step 5: Join OR which intersects AB at Q.

Now, $\overline{OQ}$ the required perpendicular from an external point O to AB.

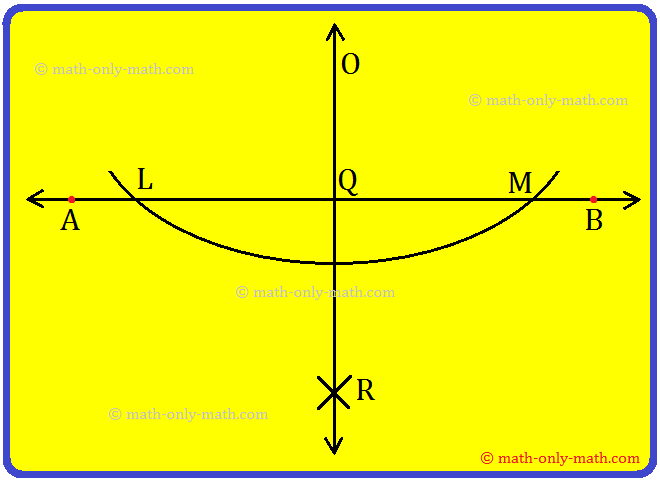
III: Construction of a Perpendicular Line by Using a Protractor:

To construct a perpendicular to a given line ℓ at a given point A on it, we need to follow the given procedure for constructing an angle of 90° at A.

Steps of construction:

1. Let ℓ be the given line and A the given point on it.

2. Place the protractor on the line ℓ such that its base line coincides with ℓ, and its centre falls on A.

3. Mark a point B against the 90° mark on the protractor.

4. Remove the protractor and draw a line m passing through A and B.

Then line m ┴ line ℓ at A.

These are the steps to construct a perpendicular.

Solved Examples on Construction of Perpendicular Lines:

1. Draw a line segment $\overline{AB}$ = 5 cm and mark a point C on AB such that $\overline{AC}$ = 3 cm. Draw a perpendicular to at C by using scale/ruler and set-square.

Solution:

It is given that $\overline{AB}$ = 5 and $\overline{AC}$ = 3 cm

Using the above Working Rules, the required perpendicular CD is drawn on AB at C,

i.e., $\overline{CD}$ ┴ $\overline{AB}$.

2. Draw a line segment CD = 7.5 cm. Mark any point P outside CD. Draw a perpendicular from P to the line segment CD and measure the perpendicular distance from P.

Solution:

Steps of Construction:

Step I: Draw $\overline{CD}$ = 7.5 cm and mark a point P outside it.

Step II: With Pas the centre and a suitable radius, draw an arc to cut $\overline{CD}$ at L and M respectively.

Step III: With L as centre and taking a radius greater than 1/2 LM, draw an arc.

Step IV: With Mas centre and the same radius as in step 3, draw another arc to cut the previous arc at R.

Step V: Join PR which intersects CD at Q. Now, $\overline{PQ}$ is the required perpendicular from an external point P to CD.

Also, PQ is the perpendicular distance from the external point P to the point Q on $\overline{CD}$. Measure PQ to find its length.

Worksheet on Construction of Perpendicular Lines:

1. How many lines can be drawn which are perpendicular to a given line and pars through a given point

(i) lying on the line?

(ii) lying outside the line?

2. Draw a line segment AB. Mark any point C, on it. Through C, draw a perpendicular $\overline{AB}$:

(i) using set-square

(ii) using compasses

3. Draw a line segment PQ = 8.5 cm and mark a point A on it such that $\overline{PA}$ = 6.5 cm. Draw a perpendicular to $\overline{PQ}$ A.

4. Draw a line segment CD = 8 cm. Mark any point P outside the $\overline{CD}$. Draw a perpendicular from P to line segment CD and measure the perpendicular distance from P.

5. Draw a line segment AB = 8.5 cm. Taking a point C on $\overline{AB}$ such that $\overline{BC}$ = 5 cm, draw a perpendicular to AB at C.

● Quadrilaterals.

Elements of a Quadrilateral.

Types of Quadrilaterals.

Parallel Lines.

Perpendicular Lines.

Construction of Perpendicular Lines by using a Protractor.

Sum of Angles of a Quadrilateral.

Worksheet on Quadrilateral.

Practice Test on Quadrilaterals.

5th Grade Geometry

5th Grade Math Problems

From Construction of Perpendicular Lines by Using a Protractor to HOME PAGE