Angle Sum Property of a Quadrilateral

Theorem and Proof of angle sum property of a quadrilateral.

Prove that the sum of all the four angles of a quadrilateral is 360°.

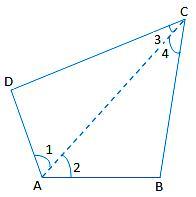
Proof: Let ABCD be a quadrilateral. Join AC.

Clearly, ∠1 + ∠2 = ∠A ...... (i)

And, ∠3 + ∠4 = ∠C ...... (ii)

We know that the sum of the angles of a triangle is 180°.

Therefore, from ∆ABC, we have

∠2 + ∠4 + ∠B = 180° (Angle sum property of triangle)

From ∆ACD, we have 

∠1 + ∠3 + ∠D = 180° (Angle sum property of triangle)

Adding the angles on either side, we get;

∠2 + ∠4 + ∠B + ∠1 + ∠3 + ∠D = 360°

⇒ (∠1 + ∠2) + ∠B + (∠3 + ∠4) + ∠D = 360°

⇒ ∠A + ∠B + ∠C + ∠D = 360° [using (i) and (ii)].

Hence, the sum of all the four angles of a quadrilateral is 360°.

Solved examples of angle sum property of a quadrilateral:

1. The angle of a quadrilateral are (3x + 2)°, (x – 3), (2x + 1)°, 2(2x + 5)° respectively. Find the value of x and the measure of each angle.

Solution:            

Using angle sum property of quadrilateral, we get

 (3x + 2)°+ (x – 3)° + (2x + 1)° +  2(2x + 5)°= 360°                 

⇒ 3x + 2 + x - 3 + 2x + 1 + 4x + 10 = 360°

⇒ 10x + 10 = 360                              

⇒ 10x = 360 – 10                              

⇒ 10x = 350                       

⇒ x = 350/10                     

⇒ x = 35                                              

Therefore, (3x + 2) = 3 × 35 + 2 = 105 + 2 = 107°

(x – 3) = 35 – 3 = 32°

(2x + 1) = 2 × 35 + 1 = 70 + 1 = 71°

2(2x + 5) = 2(2 × 35 + 5) = 2(70 + 5) = 2 × 75 = 150°

Therefore, the four angles of the quadrilateral are 32°, 71° 107°, 150° respectively.

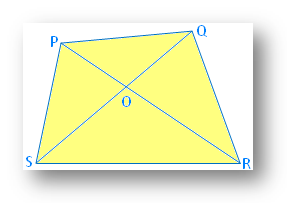
2. In a quadrilateral PQRS, PQ + QR + RS + SP < 2 (PR + QS).

Solution:            

In ∆POS, PO + OS > PS …………… (i)

In ∆SOR, SO + OR > SR …………… (ii)

In ∆QOR, QO + OR > QR …………… (iii)

In ∆POQ, PO + OQ > PQ …………… (iv)

(i) + (ii) + (iii) + (iv) (Using triangle inequality property)

PO + OS + OS + OR + OQ + OR + OP + OQ > PS + SR + QR + PQ

⇒ 2 (OP + OQ + OR + OS) > PQ + QR + CS + DP

⇒ 2 [(OP + OR) + (OQ + OS)] > PQ + QR + CS + DP

⇒ 2 (PR + QS) > PQ + QR + RS + SP

The above examples will help us to solve various types of problems based on angle sum property of a quadrilateral.

7th Grade Math Problems 

8th Grade Math Practice 

From Angle Sum Property of a Quadrilateral to HOME PAGE